题目内容
若函数f（x）=-3+
为奇函数，则实数a的值是 ．
| a |
| 2x-1 |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：函数f（x）=-3+
为奇函数，可得f（1）+f（-1）=0，解出并验证即可．
| a |
| 2x-1 |
解答：
解：∵函数f（x）=-3+
为奇函数，
可得f（1）+f（-1）=0，
∴-3+a-3-2a=0，解得a=-6．
可得f（x）=
，
经验证为奇函数．
故答案为：-6．
| a |
| 2x-1 |
可得f（1）+f（-1）=0，
∴-3+a-3-2a=0，解得a=-6．
可得f（x）=
| 3(1+2x) |
| 1-2x |
经验证为奇函数．
故答案为：-6．
点评：本题考查了奇函数的性质，属于基础题．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
现有四个函数：①y=x•sinx；②y=x•cosx；③y=x•|cosx|；④y=x•2x的图象（部分）如下：
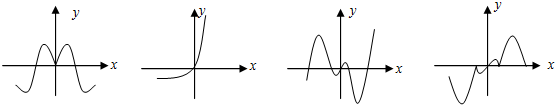
则按照从左到右图象对应的函数序号安排正确的一组是（ ）
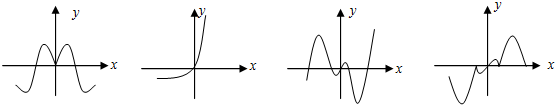
则按照从左到右图象对应的函数序号安排正确的一组是（ ）
| A、①④③② | B、③④②① |
| C、④①②③ | D、①④②③ |
已知f（x）是R上的奇函数，且f（x+4）=f（x），当x∈（0，2）时，f（x）=x2，则f（7）的值为（ ）
| A、-1 | B、4 | C、1 | D、0 |
函数y=
+log3x的定义域为（ ）
| 1-x |
| A、（-∞，1] |
| B、（0，+∞） |
| C、（0，1） |
| D、（0，1] |
若x＞0，y＞0且2x=(
)2y-1，则
+
的最小值为（ ）
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| y |
| A、3 | ||
B、2
| ||
| C、2 | ||
D、3+2
|
下列式子中，一定成立的是（ ）
| A、a•a=a2 |
| B、3a+2a2=5a3 |
| C、a3÷a2=1 |
| D、（ab）2=ab2 |