题目内容
6.三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,AC=BC=1,PA=$\sqrt{3}$,则该三棱锥外接球的表面积为5π.分析 根据题意,证出BC⊥平面PAC,PB是三棱锥P-ABC的外接球直径.利用勾股定理结合题中数据算出PB$\sqrt{5}$得外接球半径,从而得到所求外接球的表面积.
解答  解:PA⊥平面ABC,AC⊥BC,
解:PA⊥平面ABC,AC⊥BC,
∴BC⊥平面PAC,PB是三棱锥P-ABC的外接球直径;
∵Rt△PBA中,AB=$\sqrt{2}$,PA=$\sqrt{3}$,
∴PB=$\sqrt{5}$,可得外接球半径R=$\frac{1}{2}$PB=$\frac{\sqrt{5}}{2}$,
∴外接球的表面积S=4πR2=5π.
故答案为5π.
点评 本题在特殊三棱锥中求外接球的表面积,着重考查了线面垂直的判定与性质、勾股定理和球的表面积公式等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, ,
, ,则
,则 中元素的个数为( )
中元素的个数为( ) 的人数为( )
的人数为( )
 的函数
的函数 是奇函数.
是奇函数. 的值;
的值;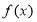 在
在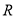 上是单调递减函数;
上是单调递减函数; ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.