题目内容
将正方体（图1）截去两个三棱锥，得到几何体（图2），则该几何体的正视图为（ ）
A、 |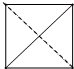
B、 |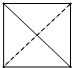
C、 |
D、 |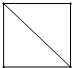
考点：简单空间图形的三视图
专题：空间位置关系与距离
分析：直接利用三视图的画法，分析正视图中，几何体棱的虚实性，画出几何体的正视图即可．
解答：
解：由题意可知几何体正视图的轮廓是正方形，
前面对角线AB′在正视图中为实线；
后面对角线CD′在正视图中为虚线；
故该几何体的正视图为：
故选：A．
前面对角线AB′在正视图中为实线；
后面对角线CD′在正视图中为虚线；
故该几何体的正视图为：
故选：A．
点评：本题考查的知识点是简单几何的三视图，熟练掌握空间几何体三视图的画法，是解答的关键．
练习册系列答案
名校课堂系列答案
相关题目
二项式（2x3-
）7的展开式中的常数项为（ ）
| 1 | ||
|
| A、16 | B、15 | C、14 | D、13 |
已知函数f（x）=sin（2x+
）（x∈R），为了得到函数g（x）=cos2x的图象，只需将y=f（x）的图象（ ）
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
集合M={x|1＜x＜2}，N={x|x＜a}，若M⊆N，则实数a的取值范围是（ ）
| A、[2，+∞） |
| B、（2，+∞） |
| C、[1，+∞） |
| D、（1，+∞） |