题目内容
求下列函数的单调区间:
(1)y=sinx,x∈[-π,π];
(2)y=cosx,x∈[-π,π];
(3)y=sinx,x∈[-π,6π];
(4)y=cosx,x∈[-
,
].
(1)y=sinx,x∈[-π,π];
(2)y=cosx,x∈[-π,π];
(3)y=sinx,x∈[-π,6π];
(4)y=cosx,x∈[-
| π |
| 3 |
| 5π |
| 6 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:(1)直接根据正弦函数的单调性确定单调区间.
(2)直接根据余弦函数的单调性确定单调区间.
(3)直接根据正弦函数的单调性确定单调区间.
(4)直接根据余弦函数的单调性确定单调区间.
(2)直接根据余弦函数的单调性确定单调区间.
(3)直接根据正弦函数的单调性确定单调区间.
(4)直接根据余弦函数的单调性确定单调区间.
解答:
解:(1)根据y=sinx的单调性:单调递增区间为:[-
,
]
单调递减区间为:[-π,-
]和[
,π]
(2)根据y=cosx的单调性:单调递增区间为:[-π,0]
单调递减区间为:[0,π]
(3)根据y=sinx的单调性:单调递增区间为:[-
,
]和[
,
]和[
,
]和
[
,6π]
单调递减区间为:[-π,-
]和[
,
]和[
,
]和[
,
]
(4)根据函数y=cosx的单调性:单调递增区间为:[
,0]
单调递减区间为:[0,
]
| π |
| 2 |
| π |
| 2 |
单调递减区间为:[-π,-
| π |
| 2 |
| π |
| 2 |
(2)根据y=cosx的单调性:单调递增区间为:[-π,0]
单调递减区间为:[0,π]
(3)根据y=sinx的单调性:单调递增区间为:[-
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
| 5π |
| 2 |
| 7π |
| 2 |
| 9π |
| 2 |
[
| 11π |
| 2 |
单调递减区间为:[-π,-
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
| 5π |
| 2 |
| 7π |
| 2 |
| 9π |
| 2 |
| 11π |
| 2 |
(4)根据函数y=cosx的单调性:单调递增区间为:[
| π |
| 3 |
单调递减区间为:[0,
| 5π |
| 6 |
点评:本题考查的知识要点:正弦函数和余弦函数的单调区间的确定.属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=
+
的值域是( )
| ||
| cosx |
| ||
| sinx |
| A、{0,2} |
| B、{-2,2} |
| C、{0,-2} |
| D、{-2,0,2} |
已知{an}是等比数列,若a6>0,则a6<a9是a6<a7的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
 如图,正三棱柱ABC-A1B1C1中,底边边长为
如图,正三棱柱ABC-A1B1C1中,底边边长为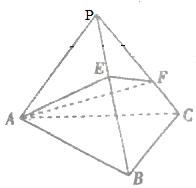 如图,在三棱锥P-ABC中,三个侧面都是顶角为20°的等腰三角形,侧棱长均为a,E、F分别是PB、PC上的点,则△AEF周长的最小值为( )
如图,在三棱锥P-ABC中,三个侧面都是顶角为20°的等腰三角形,侧棱长均为a,E、F分别是PB、PC上的点,则△AEF周长的最小值为( )