题目内容

若多项式（1-2x+3x2-4x3+…-2000x1999+2001x2000）（1+2x+3x2+4x3+…+2000x1999+2001x2000）=a0x4000+a1x3999+a2x3998+…+a3999x+a4000，则a1+a3+a5+…+a2011+a2013+a2015=
 
．
考点：二项式定理的应用
专题：计算题,二项式定理
分析：根据等式，确定a1=-2000×2001+2001×2000=0，a3=0，a5=0，…，即可得出结论．
解答： 解：根据（1-2x+3x2-4x3+…-2000x1999+2001x2000）（1+2x+3x2+4x3+…+2000x1999+2001x2000）=a0x4000+a1x3999+a2x3998+…+a3999x+a4000，
可得a1=-2000×2001+2001×2000=0，a3=0，a5=0，…，
所以a1+a3+a5+…+a2011+a2013+a2015=0，
故答案为：0．
点评：本题考查二项式定理的运用，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
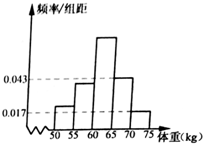某校为了解2015届高三毕业班准备考飞行员学生的身体素质，对他们的体重进行了测量，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右前3个小组的频率之比为1：2：4，其中第二小组的频率为11．
（Ⅰ）求该校报考飞行员的总人数；
（Ⅱ）若经该学校的样本数据来估计全省的总体数据，若从全省报考飞行员的学生中（人数很多）任选3人，设X表示体重超过60kg的学生人数，求X的数学期望与方差．
在区间[1，5]上任取一个数m，则函数y=x2-4x-2（0≤x≤m）的值域为[-6，-2]的概率是
 
．
一个质量为3kg的物体沿南北方向的道路（向北的方向为正方向）做直线运动，物体的位置s（单位：m）与时间t（单位：s）的关系可用函数s（t）=t-6t表示，并且物体饿动能Ek=
1
2
mv2（单位：焦耳）
（1）求瞬时速度v（单位：m/s）在t（单位：s）时刻的表达式；
（2）求物体开始运动后第5s时的动能．
已知A（3，5），B（6，9），且|
AM
|=3|
MB
|，M是直线AB上一点，求点M的坐标．
设数列{an}的前n项和为Sn，已知a1=2，a2=8，Sn+1+4Sn-1=5Sn（n≥2），Tn是数列{log2an}的前n项和，求数列{an}的通项公式．
用放缩法证明：
1
2
-
1
n+1
＜
1
22
+
1
32
+
1
n2
＜
n-1
n
（n=2，3，4…）
若函数f（x）=
x
1
2
，0≤x＜1
-
3
2
x+
5
2
，1≤x≤
5
3
的图象与x轴所围成的封闭图形的面积为a，则（x-
a
x2
）6的展开式中的常数项为
 
（用数字作答）．
执行如图所示的程序框图，则该程序运行后输出的k的值是（　　）
A、3B、4C、5D、6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网