Question

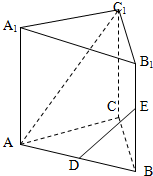如图，直三棱柱ABC-A₁B₁C₁中，AA₁=AC=AB=1，BC=

2

，D，E分别是AB，BB₁的中点，求异面直线AC₁，DE所成的角．

Answer 1

考点：异面直线及其所成的角

专题：空间角

分析：以A为原点，以AB为x轴，AC为y轴，AA₁为z轴，建立空间直角坐标系，利用向量法能求出异面直线AC₁，DE所成的角．

解答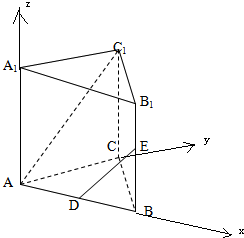： 解：∵直三棱锥ABC-A₁B₁C₁中，AA₁=AC=AB=1，BC=

2

，
∴AC²+AB²=BC²，∴AC⊥AB，
以A为原点，以AB为x轴，AC为y轴，AA₁为z轴，
建立空间直角坐标系，
∵D，E分别是AB，BB₁的中点，
∴A（0，0，0），C₁（0，1，1），
D（

1

2

，0，0），E（1，0，

1

2

），
∴

AC1

=（0，1，1），

DE

=（

1

2

，0，

1

2

），
∴cos＜

AC1

，

DE

＞=

1 2

2 • 1 2

=

1

2

，
∴异面直线AC₁，DE所成的角为60°．

点评：本题考查异面直线所成角的余弦值的求法，是中档题，解题时要认真审题，注意注意向量法的合理运用．