题目内容
已知直线l:kx-y+1=0,圆C:x2+y2-2x=0
(1)若直线l平行于直线x-ky+2=0,求k的值.
(2)若直线l和圆C相切,求k的值.
(1)若直线l平行于直线x-ky+2=0,求k的值.
(2)若直线l和圆C相切,求k的值.
考点:圆的切线方程
专题:直线与圆
分析:(1)利用直线平行的性质求解.
(2)求出圆C:x2+y2-2x=0的圆心和半径,由已知条件得圆心C(1,0)到直线直线l:kx-y+1=0的距离d=r,由此能求出k.
(2)求出圆C:x2+y2-2x=0的圆心和半径,由已知条件得圆心C(1,0)到直线直线l:kx-y+1=0的距离d=r,由此能求出k.
解答:
解:(1)∵直线l:kx-y+1=0平行于直线x-ky+2=0,
∴k=
,解得k=±1,
∴k=±1.
(2)∵圆C:x2+y2-2x=0的圆心C(1,0),半径r=
=2,
∵直线l:kx-y+1=0,圆C:x2+y2-2x=0,直线l和圆C相切,
∴圆心C(1,0)到直线直线l:kx-y+1=0的距离d=r,
即
=2,解得k=1.
∴k=
| 1 |
| k |
∴k=±1.
(2)∵圆C:x2+y2-2x=0的圆心C(1,0),半径r=
| 1 |
| 2 |
| (-2)2 |
∵直线l:kx-y+1=0,圆C:x2+y2-2x=0,直线l和圆C相切,
∴圆心C(1,0)到直线直线l:kx-y+1=0的距离d=r,
即
| |k-0+1| | ||
|
点评:本题考查实数值的求法,是基础题,解题时要认真审题,注意直线平行、直线和圆相切的性质的灵活运用.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
数列{an}中,已知对任意n∈N*,a1+a2+…+an=3n-1,则a12+a22+…+an2=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
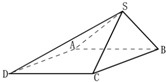 如图,设四棱锥S-ABCD的底面为菱形,且∠ABC=60°,AB=SC=2,SA=SB=
如图,设四棱锥S-ABCD的底面为菱形,且∠ABC=60°,AB=SC=2,SA=SB= 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=PD=1,CD=2.