题目内容

16．圆外切四边形的周长为48cm，相邻的三条边的比为5：4：7，求四边形各边的长．

分析 由切线长定理可得四边形的各边关系，由周长可得．

解答 解：∵四边形ABCD是圆的外切四边形，
∴AH=AE，BE=BF，CF=CG，DH=DG，
∴AH+DH+BF+CF=AE+BE+CG+DG，即AD+BC=AB+CD，
设AD=5x，DC=4x，BC=7x，则AB=8x，
∴5x+4x+7x+8x=48，解得x=2，
∴四边长分别为：10，8，14，16

点评 本题考查切线长定理，涉及三角形的知识，属基础题．

练习册系列答案
相关题目
6．已知函数y=f（x）是单调递增函数，其反函数是y=f-1（x）．
（1）若y=x2-1（x＞$\frac{1}{2}$），求y=f-1（x）并写出定义域M；
（2）对于（1）的y=f-1（x）和M，设任意x1∈M，x2∈M，x1≠x2，求证：|f-1（x1）-f-1（x2）|＜|x1-x2|；
（3）求证：若y=f（x）和y=f-1（x）有交点，那么交点一定在y=x上．
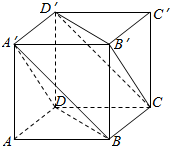7．正方体ABCD-A′B′C′D′棱长为1
（1）证明：面A′BD∥面B′CD′
（2）求点B′到面A′BD的距离．
4．已知向量$\overrightarrow{a}$=（2cosx，1），向量$\overrightarrow{b}$=（cosx，$\sqrt{3}$sin 2x），设函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$，x∈R．
（I）求函数f（x）的最小正周期；
（Ⅱ）当x∈[$-\frac{π}{6}$，$\frac{π}{3}$]时，求函数f（x）的值域．
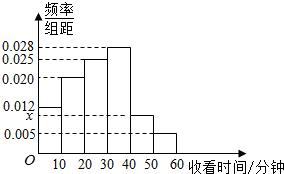11．某电视传媒公司为了了解某类体育节目的收视情况，随机抽取了100名观众进行调查，如图是根据调查结果绘制的观众日均收看该类体育节目时间的频率分布直方图，其中收看时间分组区间是：[0，10），[10，20），[20，30），[30，40），[40，50），[50，60]．则图中x的值为0.01．
1．已知函数f（x）=asin2x+bcos2x（a，b∈R，且ab≠0）的图象关于x=$\frac{π}{6}$对称，则函数y=f（x）的图象的一个对称中心是（　　）
A．（$\frac{π}{12}$，0）B．（$\frac{π}{6}$，0）C．（$\frac{π}{3}$，0）D．（$\frac{5π}{12}$，0）
8．等差数列{an}中，a2=5，a1+a5=12．
（1）求数列{an}的通项公式；
（2）设bn=2${\;}^{{a}_{n}-3}$+n，求数列{bn}的前n项和．
5．已知函数f（x）=2cos4x+2sin2x•cos2x+2$\sqrt{3}$sinx•cosx-1，x∈R．
（I）求函数f（x）的最小正周期；
（Ⅱ）设△ABC的内角A，B，C的对边分别为a，b，c，若f（π-$\frac{A}{2}$）=-1，a=2，求BC边上的高的最大值．
6．已知函数f（x）定义在（-1，1）上，对于任意的x，y∈（-1，1），有f（x）+f（y）=f（$\frac{x+y}{1+xy}$），且当x＜0时f（x）＞0．
（1）判断这样的函数是否具有奇偶性和单调性，并加以证明；
（2）若f（-$\frac{1}{2}$）=1，试解不等式2f（x）＜-1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网