题目内容
已知函数f(x)=
ax2-2lnx,a∈R.
(1)求函数f(x)的单调区间;
(2)已知点P(0,1)和函数f(x)图象上动点M(m,f(m)),对任意m∈[1,e],直线PM倾斜角都是钝角,求a的取值范围.
| 1 |
| 2 |
(1)求函数f(x)的单调区间;
(2)已知点P(0,1)和函数f(x)图象上动点M(m,f(m)),对任意m∈[1,e],直线PM倾斜角都是钝角,求a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:函数的性质及应用,导数的综合应用
分析:(1)先求函数的定义域,然后求导,利用导数大于0或导数小于0,得到关于x的不等式,解之即可;注意解不等式时要结合对应的函数图象来解;
(2)因为对任意m∈[1,e],直线PM倾斜角都是钝角,所以问题转化为导数值小于0恒成立的问题,对于导函数小于0在区间[1,e]上恒成立,则问题转化为函数的最值问题,即函数f′(x)<0恒成立,通过化简最终转化为f(m)<1在区间[1,e]上恒成立,再通过研究f(x)在[1,e]上的单调性求最值,结合(Ⅰ)的结果即可解决问题.注意分类讨论的标准的确定.
(2)因为对任意m∈[1,e],直线PM倾斜角都是钝角,所以问题转化为导数值小于0恒成立的问题,对于导函数小于0在区间[1,e]上恒成立,则问题转化为函数的最值问题,即函数f′(x)<0恒成立,通过化简最终转化为f(m)<1在区间[1,e]上恒成立,再通过研究f(x)在[1,e]上的单调性求最值,结合(Ⅰ)的结果即可解决问题.注意分类讨论的标准的确定.
解答:
解:函数f(x)的定义域为(0,+∞),f′(x)=ax-
=
,
(Ⅰ)当a<0时,f′(x)<0,故函数f(x)在(0,+∞)上单调递减;
当a=0时,f′(x)=-
<0,故函数f(x)在(0,+∞)上单调递减;
当a>0时,令f′(x)=0,结合x>0,解得x=
,当x∈(0,
)时,f′(x)<0,所以函数f(x)在(0,
)上单调递减;当x∈(
,+∞)时,f′(x)>0,所以函数f(x)在(
,+∞)上单调递增;
综上所述:当a≤0时,f′(x)<0,故函数f(x)在(0,+∞)上单调递减;当a>0时,函数f(x)在(0,
)上单调递减,在(
,+∞)上单调递增.
(Ⅱ)因为对任意m∈[1,e],直线PM的倾斜角都是钝角,所以对任意m∈[1,e],直线PM的斜率小于0,
即
<0,所以f(m)<1,即f(x)在区间[1,e]上的最大值小于1.
又因为f′(x)=ax-
=
,令g(x)=ax2-2,x∈[1,e]
(1)当a≤0时,由(Ⅰ)知f(x)在区间[1,e]上单调递减,所以f(x)的最大值为f(1)=
a<1,所以a<2,
故a≤0符和题意;
(2)当a>0时,令f′(x)=0,得x=
,
①当
≤1,即a≥2时,f(x)在区间[1,e]上单调递增,所以函数f(x)的最大值f(e)=
ae2-2<1,解得a<
,故无解;
②当
≥e,即a≤
时,f(x)在区间[1,e]上单调递减,函数f(x)的最大值为f(1)=
a<1,解得a<2,故0<a<
;
③当1<
<e,即
<a<2时,函数f(x)在(1,
)上单调递减;当x∈(
,e)上单调递增,故f(x)在区间x∈[1,e]上的最大值只能是f(1)或f(e),
所以
,即
,故
<a<
.
综上所述a的取值范围a<
.
| 2 |
| x |
| ax2-2 |
| x |
(Ⅰ)当a<0时,f′(x)<0,故函数f(x)在(0,+∞)上单调递减;
当a=0时,f′(x)=-
| 2 |
| x |
当a>0时,令f′(x)=0,结合x>0,解得x=
|
|
|
|
|
综上所述:当a≤0时,f′(x)<0,故函数f(x)在(0,+∞)上单调递减;当a>0时,函数f(x)在(0,
|
|
(Ⅱ)因为对任意m∈[1,e],直线PM的倾斜角都是钝角,所以对任意m∈[1,e],直线PM的斜率小于0,
即
| f(m)-1 |
| m |
又因为f′(x)=ax-
| 2 |
| x |
| ax2-2 |
| x |
(1)当a≤0时,由(Ⅰ)知f(x)在区间[1,e]上单调递减,所以f(x)的最大值为f(1)=
| 1 |
| 2 |
故a≤0符和题意;
(2)当a>0时,令f′(x)=0,得x=
|
①当
|
| 1 |
| 2 |
| 6 |
| e2 |
②当
|
| 2 |
| e2 |
| 1 |
| 2 |
| 2 |
| e2 |
③当1<
|
| 2 |
| e2 |
|
|
所以
|
|
| 2 |
| e2 |
| 6 |
| e2 |
综上所述a的取值范围a<
| 6 |
| e2 |
点评:本题重点考查不等式恒成立问题的基本思路,一般是转化为函数的最值问题,然后从函数的单调性入手分析,注意本题第二问讨论时的标准,一般要借助于函数图象辅助来解决问题.一方面利用了数学结合思想,同时重点考查了分类讨论思想的应用,有一定难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
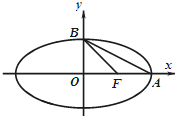 如图,椭圆C:
如图,椭圆C: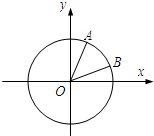 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边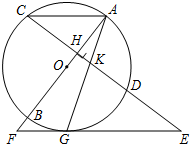 如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K,连接AC,且KG2=KD•GE.
如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K,连接AC,且KG2=KD•GE.