题目内容
已知四棱锥A-DBCE中，底面DBCE为平行四边形，F为AE的中点，求证：AB∥平面DCF．
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：连接CD，BE交于点O，连接OF，根据底面为平行四边形，判断出O为中点，推断出OF为中位线，进而可知OF∥AB，最后利用线面平行的判定定理证明出AB∥平面DCF．
解答：
证明：连接CD，BE交于点O，连接OF，
∵底面DBCE为平行四边形，
∴O为EB的中点，
∵F为AE的中点，
∴OF∥AB，
∵OF?平面DCF，AB?平面DCF，
∴AB∥平面DCF．
证明：连接CD，BE交于点O，连接OF，∵底面DBCE为平行四边形，
∴O为EB的中点，
∵F为AE的中点，
∴OF∥AB，
∵OF?平面DCF，AB?平面DCF，
∴AB∥平面DCF．
点评：本题主要考查了线面平行的判定定理的运用．解题过程中作出CD，BE的辅助线是解题的关键．
练习册系列答案
相关题目
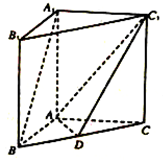如图，在直三棱柱ABC-A1B1C1中，点D是BC的中点．
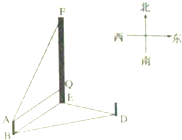如图所示，要测量山高EF，把测量仪器放到点B处得到数据∠FAQ=75°，点E位于点B的北偏东60°方向上，从点B沿北偏东75°方向前行30m到达点D，利用仪器测得点E在点D的北偏西60°方向上，求山高EF．（已知仪器高2m）