题目内容
13.设数列{an}满的前n项和为Sn,且Sn+an=2,n∈N*.(1)求数列{an}的通项公式;
(2)设${b_n}=\frac{1}{{{{log}_2}{a_{n+1}}{{log}_2}{a_{n+2}}}}$,求数列{$\frac{1}{{n{b_n}}}$}的前n项和Tn.
分析 (1)n=1时,S1+a1=2,求出a1=1,n≥2时,Sn+an-Sn-1-an-1=0,求出$\frac{a_n}{{{a_{n-1}}}}=\frac{1}{2}$,由此能求出数列{an}的通项公式.
(2)由已知推导出$\frac{1}{n{b}_{n}}$=n+1,由此能求出数列{$\frac{1}{{n{b_n}}}$}的前n项和.
解答 解:(1)∵数列{an}满的前n项和为Sn,且Sn+an=2,n∈N*.
∴n=1时,S1+a1=2,解得a1=1,
n≥2时,Sn+an-Sn-1-an-1=0,
∴2an=an-1,∵a1=1≠0,∴$\frac{a_n}{{{a_{n-1}}}}=\frac{1}{2}$,
∴数列{an}是首项为1,公比为$\frac{1}{2}$的等比数列.
∴${a_n}={({\frac{1}{2}})^{n-1}}$.
(2)∵${b_n}=\frac{1}{{{{log}_2}{a_{n+1}}{{log}_2}{a_{n+2}}}}$=$\frac{1}{lo{g}_{2}(\frac{1}{2})^{n}•lo{g}_{2}(\frac{1}{2})^{n+1}}$=$\frac{1}{n(n+1)}$,
∴$\frac{1}{n{b}_{n}}$=n+1,
∴数列{$\frac{1}{{n{b_n}}}$}的前n项和:
Tn=2+3+4+…n+(n+1)=$\frac{n(n+3)}{2}$.
点评 本题考查数列的通项公式的求法,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
6.在下面选项中,是x2-y2<0表示的平面区域是( )
| A. |  | B. |  | C. |  | D. |  |
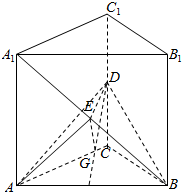 如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.
如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.