题目内容
已知函数f（x）=2（sinx-cosx）cosx．
（1）求f（x）的最小正周期；
（2）求f（x）的单调递增区间．
（1）求f（x）的最小正周期；
（2）求f（x）的单调递增区间．
考点：三角函数中的恒等变换应用,正弦函数的图象
专题：三角函数的求值
分析：（1）化简可得f（x）=
sin（2x-
）-1，由周期公式可得；（2）由2kπ-
≤2x-
≤2kπ+
解不等式可得函数的单调区间．
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
解答：
解：（1）化简可得f（x）=2（sinx-cosx）cosx
=2sinxcosx-2cos2x=sin2x-1-cos2x
=
sin（2x-
）-1
∴函数f（x）的最小正周期为T=
=π
（2）由2kπ-
≤2x-
≤2kπ+
可得-
+kπ≤x≤
+kπ，
∴原函数的单调递增区间为：[-
+kπ，
+kπ]（k∈Z）
=2sinxcosx-2cos2x=sin2x-1-cos2x
=
| 2 |
| π |
| 4 |
∴函数f（x）的最小正周期为T=
| 2π |
| 2 |
（2）由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| 3π |
| 8 |
∴原函数的单调递增区间为：[-
| π |
| 8 |
| 3π |
| 8 |
点评：本题考查三角函数的化简，涉及三角函数的周期性和单调性，属基础题．
练习册系列答案
相关题目
在数学归纳法的递推性证明中由假设n=k时成立推导n=k+1时成立时f（n）=1+
+
+…+
增加的项数是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n-1 |
| A、1 |
| B、2k+1 |
| C、2k-1 |
| D、2k |
已知圆锥母线长为6，底面圆半径长为4，点M是母线PA的中点，AB是底面圆的直径，半径OC与母线PB所成的角的大小等于60°．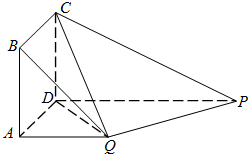
在如图所示的多面体中，四边形ABCD为正方形，四边形ADPQ是直角梯形，AD⊥DP，CD⊥平面PDAQ，AB=AQ=
根据如图所示的程序框图，将输出的x、y值依次分别记为x1，x2，…，xn，…，x2007；y1，y2，…，yn…，y2007；
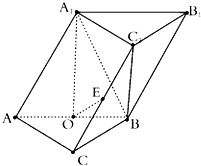三棱柱ABC-A1B1C1，平面A1ABB1⊥平面ABC，AA1=AB=2，∠A1AB=60°，AC=BC=