Question

扇形AOB中心角为60°，所在圆半径为

3

，它按如下（Ⅰ）（Ⅱ）两种方式有内接矩形CDEF．
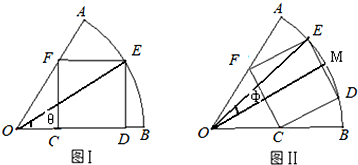
（Ⅰ）矩形CDEF的顶点C、D在扇形的半径OB上，顶点E在圆弧AB上，顶点F在半径OA上，设∠EOB=θ；
（Ⅱ）点M是圆弧AB的中点，矩形CDEF的顶点D、E在圆弧AB上，且关于直线OM对称，顶点C、F分别在半径OB、OA上，设∠EOM=φ；
试研究（Ⅰ）（Ⅱ）两种方式下矩形面积的最大值，并说明两种方式下哪一种矩形面积最大？

Answer 1

考点：解三角形的实际应用,扇形面积公式,三角函数中的恒等变换应用,三角函数的最值

专题：三角函数的图像与性质

分析：（Ⅰ）如图先用所给的角将矩形的面积表示出来，建立三角函数模型，再根据所建立的模型利用三角函数的性质求最值．
（Ⅱ）先用所给的角将矩形的面积表示出来，建立三角函数模型，再根据所建立的模型利用三角函数的性质求最值．然后比较面积的最大值，得到结果即可．

解答： 解：如图，在Rt△OD中，设∠EOD=θ，则OD=

3

cosθ，ED=

3

sinθ
又CD=OD-OC=

3

cosθ-

CF

tan60°

=

3

cosθ-sinθ，
∴S_CDEF=ED•CD=

3

sinθ（

3

cosθ-sinθ）
=3sinθcosθ-

3

sin²θ
=

3

2

sin2θ-

3

2

(1-cos2θ)
=

3

sin（2θ+

π

6

）-

3

2

．
当2θ+

π

6

=

π

2

，即θ=

π

6

时，S_最大=

3

2

．
（Ⅱ）令ED与OM的交点为N，FC与OM的交点为P，则EN=

3

sinφ，
于是ED=2

3

sinφ，又CD=PN=ON-OP=

3

cosφ-

FP

tan30°

=

3

cos-3sinφ，
∴S_CDEF=ED•CD=2

3

sinφ（

3

cosφ-3sinφ）=3sin2φ-3

3

（1-cos2φ）=6sin（2φ+

π

3

）-3

3

．
当22φ+

π

3

=

π

2

，即φ=

π

12

时，y取得最大值为：6-3

3

．
∵

3

2

＞6-3

3

，（Ⅰ）（Ⅱ）两种方式下矩形面积的最大值为方式（Ⅱ）．

点评：本题考查在实际问题中建立三角函数模型，求解问题的关键是根据图形建立起三角模型，将三角模型用所学的恒等式变换公式进行化简．