题目内容
已知函数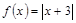 ,
,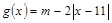 , 若
, 若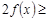
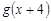 恒成立,实数
恒成立,实数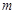 的最大值为
的最大值为 .
.
(1)求实数 .
.
(2)已知实数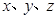 满足
满足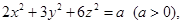 且
且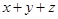 的最大值是
的最大值是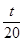 ,求
,求 的值.
的值.
(Ⅰ)20;(Ⅱ)1.
解析试题分析:(Ⅰ)若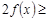
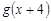 恒成立,代入函数利用绝对值不等式求
恒成立,代入函数利用绝对值不等式求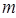 得最大值;(Ⅱ)由柯西不等式求解.
得最大值;(Ⅱ)由柯西不等式求解.
试题解析:(Ⅰ)函数 的图象恒在函数
的图象恒在函数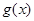 图象的上方,
图象的上方,
即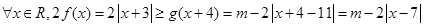 , 1分
, 1分
从而有 , 2分
, 2分
由绝对值不等式的性质可知 ,
,
因此,实数 的最大值
的最大值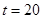 . 3分
. 3分
(Ⅱ)由柯西不等式: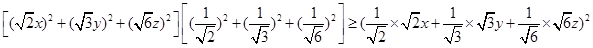 ,5分
,5分
因为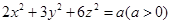 ,所以
,所以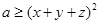 ,
,
因为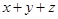 的最大值是1,所以
的最大值是1,所以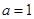 ,当
,当 时,
时,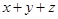 取最大值, 6分
取最大值, 6分
所以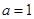 . 7分
. 7分
考点:1、绝对值不等式;2、柯西不等式.

练习册系列答案
相关题目
 的不等式
的不等式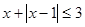 ;
;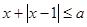 有解,求实数
有解,求实数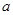 的取值范围.
的取值范围.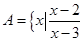 <
<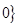 ,
,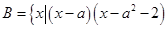 <
< 时,求
时,求 ;
;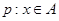 ,命题
,命题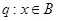 ,若q是p的必要条件,求实数
,若q是p的必要条件,求实数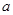 的取值范围.
的取值范围.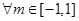 ,不等式a2-5a-3≥
,不等式a2-5a-3≥ 恒成立,若命题“P或Q”为真命题,且“P且Q”为假命题,求实数a的范围。
恒成立,若命题“P或Q”为真命题,且“P且Q”为假命题,求实数a的范围。 ,
,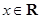 .
.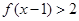 ;
;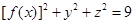 ,试求
,试求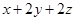 的最小值.
的最小值.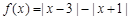 ,
,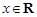 .
. ;
;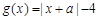 ,且
,且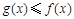 在
在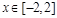 上恒成立,求实数
上恒成立,求实数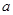 的取值范围.
的取值范围.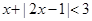

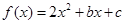 ,不等式
,不等式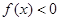 的解集是
的解集是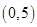 ,
,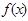 的解析式;
的解析式;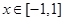 ,不等式
,不等式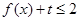 恒成立,求t的取值范围.
恒成立,求t的取值范围.