题目内容
(本小题满分12分)
已知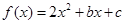 ,不等式
,不等式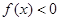 的解集是
的解集是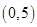 ,
,
(Ⅰ) 求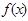 的解析式;
的解析式;
(Ⅱ) 若对于任意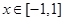 ,不等式
,不等式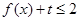 恒成立,求t的取值范围.
恒成立,求t的取值范围.
(1) (2)
(2)
解析试题分析:(1)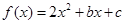 ,不等式
,不等式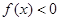 的解集是
的解集是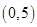 ,
,
所以 的解集是
的解集是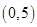 ,
,
所以 是方程
是方程 的两个根,
的两个根,
由韦达定理知,
 . ……4分
. ……4分
(2)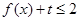 恒成立等价于
恒成立等价于 恒成立,
恒成立,
所以 的最大值小于或等于
的最大值小于或等于 .
.
设 ,
,
则由二次函数的图象可知 在区间
在区间 为减函数,
为减函数,
所以 ,所以
,所以 . ……12分
. ……12分
考点:本小题主要考查不等式的解集与方程根的关系、方程根与系数的关系和不等式恒成立问题,考查学生灵活转化问题进行求解的能力.
点评:恒成立问题是平时考查和高考考查的重点题型,恒成立问题一般都转化成求函数的最值问题来解决,当然转化之前应该先想办法把参数分离开.

练习册系列答案
相关题目
函数 的图像恒过定点A,若点A在直线
的图像恒过定点A,若点A在直线 上,其中
上,其中 的最小值为( )
的最小值为( )
| A.6 | B.8 | C.4 | D.10 |
函数y= (x>-1)的图象最低点的坐标为( )
(x>-1)的图象最低点的坐标为( )
| A.(1,2) | B.(1,-2) | C.(1,1) | D.(0,2) |
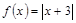 ,
,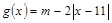 , 若
, 若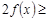
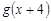 恒成立,实数
恒成立,实数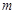 的最大值为
的最大值为 .
.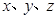 满足
满足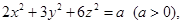 且
且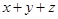 的最大值是
的最大值是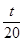 ,求
,求 的值.
的值.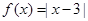 ,
,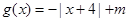
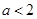 ,解关于
,解关于 的不等式
的不等式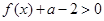 ;
; 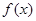 的图象恒在函数
的图象恒在函数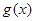 图象的上方,求实数
图象的上方,求实数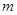 的取值范围.
的取值范围.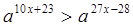
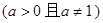 中的x的取值范围.
中的x的取值范围.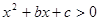 的解集为
的解集为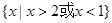
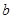 和
和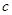 的值; (2)求不等式
的值; (2)求不等式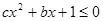 的解集.
的解集. 的一元二次不等式
的一元二次不等式
 时,求不等式
时,求不等式 取什么值时,关于
取什么值时,关于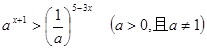 ,求
,求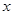 的取值范围.
的取值范围.