题目内容
一个袋中装有形状大小完全相同的球9个,其中红球3个,白球6个,每次随机取1个,直到取出3次红球即停止.
(Ⅰ)从袋中不放回地取球,求恰好取4次停止的概率P1;
(Ⅱ)从袋中有放回地取球.
①求恰好取5次停止的概率P2;
②记5次之内(含5次)取到红球的个数为ξ,求随机变量ξ的分布列及数学期望.
(Ⅰ)从袋中不放回地取球,求恰好取4次停止的概率P1;
(Ⅱ)从袋中有放回地取球.
①求恰好取5次停止的概率P2;
②记5次之内(含5次)取到红球的个数为ξ,求随机变量ξ的分布列及数学期望.
考点:离散型随机变量的期望与方差,排列、组合及简单计数问题
专题:概率与统计
分析:(Ⅰ)利用古典概型的概率计算公式能求出恰好取4次停止的概率P1.
(Ⅱ)①利用n次独立重复试验概率公式能求出恰好取5次停止的概率P2.
②由题意知随机变量ξ的取值为0,1,2,3,分别求出相对应的概率,由此能求出随机变量ξ的分布列及数学期望.
(Ⅱ)①利用n次独立重复试验概率公式能求出恰好取5次停止的概率P2.
②由题意知随机变量ξ的取值为0,1,2,3,分别求出相对应的概率,由此能求出随机变量ξ的分布列及数学期望.
解答:
解:(Ⅰ)恰好取4次停止的概率:
P1=(
×
×
+
×
×
+
×
×
)×
=
.
(Ⅱ)①恰好取5次停止的概率P2=
×(
)2×(
)2×
=
.
②由题意知随机变量ξ的取值为0,1,2,3,
由n次独立重复试验概率公式Pn(k)=
pk(1-p)n-k,得
P(ξ=0)=
×(1-
)5=
,
P(ξ=1)=
×
×(1-
)4=
,
P(ξ=2)=
×(
)2(1-
)3 =
,
ξ=3这个事件包括了三种情况,第一种取三次取到全是红球,第二种取四次取到三次红球,此时,第四次一定取到红球,前三次两次取到红球,第三种取五次取到三个红球,第五次取到的是红球,前四次取到两次红球,故有
P(ξ=3)=(
)3+
×(
)3×(1-
)+
×(
)3×(1-
)2=
,
∴ξ的分布列为:
∴Eξ=0×
+1×
+2×
+3×
=
.
P1=(
| 6 |
| 9 |
| 3 |
| 8 |
| 2 |
| 7 |
| 3 |
| 9 |
| 6 |
| 8 |
| 2 |
| 7 |
| 3 |
| 9 |
| 2 |
| 8 |
| 6 |
| 7 |
| 1 |
| 6 |
| 1 |
| 28 |
(Ⅱ)①恰好取5次停止的概率P2=
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 81 |
②由题意知随机变量ξ的取值为0,1,2,3,
由n次独立重复试验概率公式Pn(k)=
| C | k n |
P(ξ=0)=
| C | 0 5 |
| 1 |
| 3 |
| 32 |
| 243 |
P(ξ=1)=
| C | 1 5 |
| 1 |
| 3 |
| 1 |
| 3 |
| 80 |
| 243 |
P(ξ=2)=
| C | 2 5 |
| 1 |
| 3 |
| 1 |
| 3 |
| 80 |
| 243 |
ξ=3这个事件包括了三种情况,第一种取三次取到全是红球,第二种取四次取到三次红球,此时,第四次一定取到红球,前三次两次取到红球,第三种取五次取到三个红球,第五次取到的是红球,前四次取到两次红球,故有
P(ξ=3)=(
| 1 |
| 3 |
| C | 1 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| C | 2 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| 51 |
| 243 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 32 |
| 243 |
| 80 |
| 243 |
| 80 |
| 243 |
| 51 |
| 243 |
| 131 |
| 81 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要注意n次独立重复试验概率公式的灵活运用.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
已知|
|=1,|
|=2且(
+
)与
垂直,则
与
的夹角是( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、60° | B、90° |
| C、135° | D、120° |
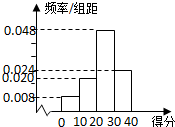 对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图所示,列出乙的得分统计表如下:
对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图所示,列出乙的得分统计表如下:
 有一个奇数组成的数阵排列如图:则第30行从左到右第3个数是
有一个奇数组成的数阵排列如图:则第30行从左到右第3个数是