题目内容

已知在二阶矩阵M的作用下，点P（1，3）变化为点P1（10，6），点Q（2，1）变化为Q1（5，2）．求二阶矩阵M．
考点：二阶矩阵
专题：计算题
分析：先设出所求矩阵，根据点的列向量在矩阵的作用下变为另一列向量，建立一个四元一次方程组，解方程组即可．
解答： 解：设M=
ab
cd
，则有
ab
cd
 
1 
3 
=
10 
6 
，
ab
cd
 
2 
1 
=
5 
2 
，
∴
a+3b=10
c+3d=6
2a+b=5
2c+d=2
，解得：
a=1
b=3
c=0
d=2
，
∴M=
13
02
．
点评：本题主要考查了二阶矩阵，以及待定系数法等有关知识，同时考查了运算求解的能力，属于基础题．
练习册系列答案
相关题目
110（2）=
 
．
已知圆C的圆心为（2，-1）且该圆被直线l：x-y-1=0截得的弦长为2
2
，求该圆的方程及过弦的两端点且面积最小的圆的方程．
已知O是坐标原点，点A（2，0），△AOC的顶点C在曲线y2=4（x-1）上，那么△AOC的重心G的轨迹方程是（　　）
A、3y2=4（x-1）
B、3y2=4（x-1）（y≠0）
C、
y2
3
=4（x-1）
D、
y2
3
=4（x-1）（y≠0）
在面积为9的正方形ABCD内部随机取一点P，则能使△PAB的面积大于3的概率是（　　）
A、
1
3
B、
2
3
C、
1
9
D、
8
9
某医院有内科医生12名，外科医生8名，现选派5名参加赈灾医疗队
（1）某内科医生甲与某外科医生乙必须参加，共有多少种不同选法？
（2）甲、乙均不能参加，有多少种选法？
（3）甲、乙两人至少有一人参加，有多少种选法？
（4）队中至少有一名内科医生和一名外科医生，有几种选法？
已知定点A（4，2），O为坐标原点，P是线段OA的垂直平分线上一点，若∠OPA≥60°，则点P横坐标的取值范围为
 
．
已知点P（x，y）满足x2+y2-2y=0，则u=
y+1
x
的取值范围是（　　）
A、-
3
≤μ≤
3
B、μ≤-
3
或μ≥
3
C、-
3
3
≤μ≤
3
3
D、μ≤-
3
3
或μ≥
3
3
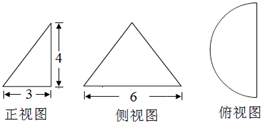某几何体的三视图如图所示（单位：cm），则其体积和表面积分别是（　　）
A、6πcm3和12（1+π）cm2
B、6πcm3和12πcm2
C、12πcm3和12（1+π）cm2
D、12πcm3和12πcm2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网