题目内容
已知函数f(x)=msinx-cosx,若x0是函数f(x)的一个极值点,且cos2x0=-
,则m的值为( )
| 3 |
| 5 |
| A、1 | B、±1 | C、2 | D、±2 |
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:求出函数的导数,得到函数的极值点,利用二倍角公式以及同角三角函数的基本关系式化简求解即可.
解答:
解:函数f(x)=msinx-cosx,
可得f′(x)=mcosx+sinx,
∵x0是函数f(x)的一个极值点,
∴mcosx0=-sinx0,
又cos2x0=-
,
可得
=-
,
=-
,
即
=-
,
解得m=±2.
故选:D.
可得f′(x)=mcosx+sinx,
∵x0是函数f(x)的一个极值点,
∴mcosx0=-sinx0,
又cos2x0=-
| 3 |
| 5 |
可得
| cos2x0-sin2x0 |
| sin2x0+cos2x0 |
| 3 |
| 5 |
| cos2x0-m2cos2x0 |
| m2cos2x0+cos2x0 |
| 3 |
| 5 |
即
| 1-m2 |
| m2+1 |
| 3 |
| 5 |
解得m=±2.
故选:D.
点评:本题考查函数的导数的应用,三角函数的化简求值,考查分析问题解决问题的能力.

练习册系列答案
相关题目
若|
+
|=|
-
|=2|
|,则向量
+
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现双方各出上、中、下等马各一匹分组分别进行一场比赛,胜两场及以上者获胜,若双方均不知道对方马的出场顺序,则田忌获胜的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
| OA, |
| OB |
| OA |
| OB |
| OM |
| OA |
| ON |
| OB |
| MN |
| 2 |
| 7 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
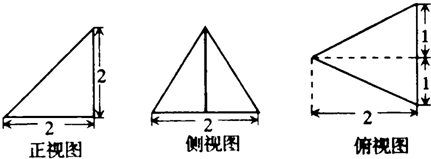
已知某个几何体的三视图如图所示.根据图中标出的尺寸(单位:cm).可得这个几何体的体积是 cm3.
( )
( )

A、
| ||||
B、
| ||||
C、
| ||||
| D、4 |
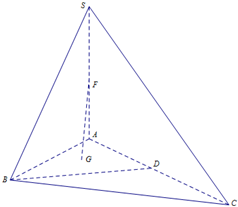 在三棱锥S-ABC中,SA⊥平面ABC,AB⊥AC.
在三棱锥S-ABC中,SA⊥平面ABC,AB⊥AC.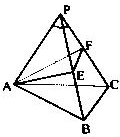 如图,三棱锥P-ABC中,∠APB=∠BPC=∠CPA=30°PA=PB=PC=a,E,F分别为PB,PC上的点,则△AEF周长的最小值等于 ( )
如图,三棱锥P-ABC中,∠APB=∠BPC=∠CPA=30°PA=PB=PC=a,E,F分别为PB,PC上的点,则△AEF周长的最小值等于 ( )