题目内容
已知k∈[-2,2],则k的值使得过点A(0,2)可以作2条直线与圆x2+y2+kx-2y+
k=0相切的概率为( )
| 5 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:把圆的方程化为标准方程后,根据构成圆的条件得到等号右边的式子大于0,列出关于k的不等式,求出不等式的解集,然后由过已知点总可以作圆的两条切线,得到点在圆外,故把点的坐标代入圆的方程中得到一个关系式,让其大于0列出关于k的不等式,求出不等式的解集,综上,求出两解集的并集即为实数k的取值范围.最后利用几何概型的计算公式求解即得.
解答:
解:把圆的方程化为标准方程得:(x+
k)2+(y-1)2=
k2-
k+1,
所以
k2-
k+1>0,解得:k>4或k<1,
又点A(0,2)应在已知圆的外部,
把点代入圆方程得:4-4+
k>0,解得:k>0,
则实数k的取值范围是(0,1).
任取k∈[-2,2],
则k的值使得过A(0,2)可以作两条直线与圆x2+y2+kx-2y+
k=0相切的概率为P=
=
,
故选:D.
| 1 |
| 2 |
| 1 |
| 4 |
| 5 |
| 4 |
所以
| 1 |
| 4 |
| 5 |
| 4 |
又点A(0,2)应在已知圆的外部,
把点代入圆方程得:4-4+
| 5 |
| 4 |
则实数k的取值范围是(0,1).
任取k∈[-2,2],
则k的值使得过A(0,2)可以作两条直线与圆x2+y2+kx-2y+
| 5 |
| 4 |
| 1-0 |
| 2-(-2) |
| 1 |
| 4 |
故选:D.
点评:此题考查了几何概型,点与圆的位置关系,二元二次方程为圆的条件及一元二次不等式的解法.理解过已知点总利用作圆的两条切线,得到把点坐标代入圆方程其值大于0是解本题的关键.

练习册系列答案
相关题目
已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程是( )
| A、(x+1)2+y2=2 |
| B、(x+1)2+y2=8 |
| C、(x-1)2+y2=2 |
| D、(x-1)2+y2=8 |
给出程序框图,若输入的x值为-5,则输出的y的值是( )


| A、-2 | B、-1 | C、0 | D、1 |
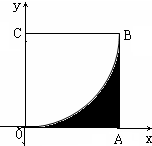 如图,已知正方形OABC的四个顶点坐标分别为O(0,0),A(1,0),B(1,1),C(0,1),现向该正方体内部随机投1000个点,统计出所投点落在阴影部分的个数为328,由此估计图中阴影部分的面积为( )
如图,已知正方形OABC的四个顶点坐标分别为O(0,0),A(1,0),B(1,1),C(0,1),现向该正方体内部随机投1000个点,统计出所投点落在阴影部分的个数为328,由此估计图中阴影部分的面积为( ) 如图,
如图,