题目内容
下列四种说法
①若复数z满足方程z2+2=0,则z3=-2
i;
②若S1=
x2dx,S2=
dx,S3=
exdx,则三者的大小关系为S3<S2<S1;
③若(1-2x)2012=a0+a1x+…+a2012x2012(x∈R),则
+
+…+
=-1;
④用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)(n∈N*)时,从“k”到“k+1”的证明,左边需增添的一个因式是2(2k+1).其中正确的是( )
①若复数z满足方程z2+2=0,则z3=-2
| 2 |
②若S1=
| ∫ | 2 1 |
| ∫ | 2 1 |
| 1 |
| x |
| ∫ | 2 1 |
③若(1-2x)2012=a0+a1x+…+a2012x2012(x∈R),则
| a1 |
| 2 |
| a2 |
| 22 |
| a2012 |
| 22012 |
④用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)(n∈N*)时,从“k”到“k+1”的证明,左边需增添的一个因式是2(2k+1).其中正确的是( )
| A、①② | B、③ | C、③④ | D、④ |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①由复数z满足方程z2+2=0,则z=±
i,可得z3=±2
i;
②利用微积分基本定理可得S1=
=
;S2=lnx
=ln2;S3=ex
=e2-e.即可比较出大小;
③由(1-2x)2012=a0+a1x+…+a2012x2012(x∈R),令x=0,则a0=1.令x=
,则0=a0+
+
+…+
,即可得出;
④用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)(n∈N*)时,从“k”到“k+1”的证明,左边需增添的一个因式是
.
| 2 |
| 2 |
②利用微积分基本定理可得S1=
| x3 |
| 3 |
| | | 2 1 |
| 7 |
| 3 |
| | | 2 1 |
| | | 2 1 |
③由(1-2x)2012=a0+a1x+…+a2012x2012(x∈R),令x=0,则a0=1.令x=
| 1 |
| 2 |
| a1 |
| 2 |
| a2 |
| 22 |
| an |
| 2n |
④用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)(n∈N*)时,从“k”到“k+1”的证明,左边需增添的一个因式是
| (k+1+k)(k+1+k+1) |
| k+1 |
解答:
解:①若复数z满足方程z2+2=0,则z=±
i,∴z3=±2
i,因此①不正确;
②∵S1=
x2dx,∴S1=
=
;S2=
dx=lnx
=ln2;S3=
exdx=ex
=e2-e.
∵e2-e>
>ln2,∴三者的大小关系为S3>S1>S2,因此不正确;
③由(1-2x)2012=a0+a1x+…+a2012x2012(x∈R),令x=0,则a0=1.令x=
,则0=a0+
+
+…+
,
则
+
+…+
=-a1=-1,因此正确;
④用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)(n∈N*)时,从“k”到“k+1”的证明,左边需增添的一个因式是
即
2(2k+1).
其中正确的是③④.
故选:C.
| 2 |
| 2 |
②∵S1=
| ∫ | 2 1 |
| x3 |
| 3 |
| | | 2 1 |
| 7 |
| 3 |
| ∫ | 2 1 |
| 1 |
| x |
| | | 2 1 |
| ∫ | 2 1 |
| | | 2 1 |
∵e2-e>
| 7 |
| 3 |
③由(1-2x)2012=a0+a1x+…+a2012x2012(x∈R),令x=0,则a0=1.令x=
| 1 |
| 2 |
| a1 |
| 2 |
| a2 |
| 22 |
| an |
| 2n |
则
| a1 |
| 2 |
| a2 |
| 22 |
| a2012 |
| 22012 |
④用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)(n∈N*)时,从“k”到“k+1”的证明,左边需增添的一个因式是
| (k+1+k)(k+1+k+1) |
| k+1 |
2(2k+1).
其中正确的是③④.
故选:C.
点评:本题考查了复数的运算法则、微积分基本定理、二项式定理的应用、数学归纳法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
函数y=x-
的导数是( )
| 1 |
| x |
A、1-
| ||
B、1-
| ||
C、1+
| ||
D、1+
|
设
与
都是单位向量,则下列各式中成立的是( )
| a |
| b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、|
|
设f(sinα+cosα)=sin2α,则f(
)的值为( )
| 1 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
下列命题中为真命题的是( )
| A、若数列{an}为等比数列的充要条件是an2=an-1•an+1 |
| B、“a=1是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件 |
| C、若命题p:“?x∈R,x2-x-1>0”,则命题的否定为:“?x∈R,x2-x-1≤0” |
| D、直线a,b为异面直线的充要条件是直线a,b不相交 |
若3sinx-
cosx=2
sin(x-φ),φ∈(-π,π),则φ=( )
| 3 |
| 3 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
-401是等差数列-5,-9,-13…的第( )项.
| A、98 | B、99 |
| C、100 | D、101 |
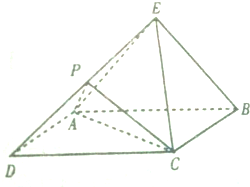 如图,设四棱锥E-ABCD的底面为菱形,且∠ABC=60°,P为DE上一点 若BE∥平面PAC.
如图,设四棱锥E-ABCD的底面为菱形,且∠ABC=60°,P为DE上一点 若BE∥平面PAC.