题目内容
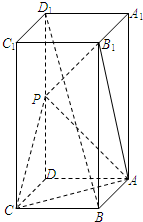 如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=2AB,且点P为DD1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=2AB,且点P为DD1的中点.(1)求证:直线BD1∥平面PAC;
(2)求证:平面PB1A⊥平面PAC.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)连结BD交AC于点O,由三棱柱ABC-A1B1C1为正三棱柱,可知四边形ABCD是正方形,所以O是BD的中点,又点P是DD1的中点,进而可知PO∥BD1,利用线面平行的判定定理推断出直线BD1∥平面PAC;
(2)连结B1O,设AA1=2AB=2a,在三角形PB1O中,分别求得B1P2,B1O2,PO2,进而可知PO2+B1P2=B1O2,即PB1⊥PO,又三棱柱ABC-A1B1C1为正三棱柱,推断出AC⊥BD,B1B⊥平面ABCD,进而根据线面垂直的性质知AC⊥BB1,推断出AC⊥平面BD1D,可知B1P⊥AC,利用线面垂直的判定定理推断出B1P⊥平面PAC,最后根据面面垂直的判定定理推断出平面PB1A⊥平面PAC.
(2)连结B1O,设AA1=2AB=2a,在三角形PB1O中,分别求得B1P2,B1O2,PO2,进而可知PO2+B1P2=B1O2,即PB1⊥PO,又三棱柱ABC-A1B1C1为正三棱柱,推断出AC⊥BD,B1B⊥平面ABCD,进而根据线面垂直的性质知AC⊥BB1,推断出AC⊥平面BD1D,可知B1P⊥AC,利用线面垂直的判定定理推断出B1P⊥平面PAC,最后根据面面垂直的判定定理推断出平面PB1A⊥平面PAC.
解答:
证明:(1)连结BD交AC于点O,
因为三棱柱ABC-A1B1C1为正三棱柱,
所以四边形ABCD是正方形,所以E是BD的中点,
又点P是DD1的中点,
所以PO∥BD1,
而BD1?平面PAC,PO?平面PAC,
所以直线BD1∥平面PAC;
(2)连结B1O,设AA1=2AB=2a,
在三角形PB1O中,B1P2=3a2,B1O2=
a2,
所以PO2+B1P2=B1O2,
所以PB1⊥PO,
因为三棱柱ABC-A1B1C1为正三棱柱,所以AC⊥BD,B1B⊥平面ABCD,
而AC?平面ABCD,所以AC⊥BB1,
又BD∩BB1=B,所以AC⊥平面BD1D,
因B1P?平面BD1D,所以B1P⊥AC,
又PO∩AC=O,
所以B1P⊥平面PAC,
又PB1?PB1A,
所以平面PB1A⊥平面PAC.
因为三棱柱ABC-A1B1C1为正三棱柱,
所以四边形ABCD是正方形,所以E是BD的中点,
又点P是DD1的中点,
所以PO∥BD1,
而BD1?平面PAC,PO?平面PAC,
所以直线BD1∥平面PAC;
(2)连结B1O,设AA1=2AB=2a,
在三角形PB1O中,B1P2=3a2,B1O2=
| 9 |
| 2 |
所以PO2+B1P2=B1O2,
所以PB1⊥PO,
因为三棱柱ABC-A1B1C1为正三棱柱,所以AC⊥BD,B1B⊥平面ABCD,
而AC?平面ABCD,所以AC⊥BB1,
又BD∩BB1=B,所以AC⊥平面BD1D,
因B1P?平面BD1D,所以B1P⊥AC,
又PO∩AC=O,
所以B1P⊥平面PAC,
又PB1?PB1A,
所以平面PB1A⊥平面PAC.
点评:本题主要考查了面面垂直的判定定理的应用,线面平行的判定定理的应用.要求学生能对基础的定理能熟练记忆.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在等差数列{an}中,若a3+a6+a9=90,则S11等于( )
| A、270 | B、300 |
| C、330 | D、360 |
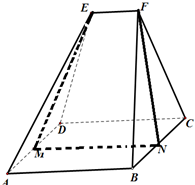 木工技艺是我国传统文化瑰宝之一,体现了劳动人民的无穷智慧.很多古代建筑和家具不用铁钉,保存到现代却依然牢固,这其中,有连接加固功能的“楔子”发挥了重要作用;如图,是一个楔子形状的直观图.其底面ABCD为一个矩形,其中AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6
木工技艺是我国传统文化瑰宝之一,体现了劳动人民的无穷智慧.很多古代建筑和家具不用铁钉,保存到现代却依然牢固,这其中,有连接加固功能的“楔子”发挥了重要作用;如图,是一个楔子形状的直观图.其底面ABCD为一个矩形,其中AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6