题目内容
在△ABC中,角A,B,C所对应的边分别为a,b,c.若a,b是方程x2-2
x+2=0的两根,且2cos(A+B)=1.
(1)求角C的度数;
(2)求c;
(3)求△ABC的面积.
| 3 |
(1)求角C的度数;
(2)求c;
(3)求△ABC的面积.
考点:正弦定理,两角和与差的余弦函数
专题:计算题,解三角形
分析:(1)由A+B=180-C及诱导公式可求C;
(2)韦达定理及余弦公式可求c;
(3)利用面积公式S=
absinC可求;
(2)韦达定理及余弦公式可求c;
(3)利用面积公式S=
| 1 |
| 2 |
解答:
解:(1)由2cos(A+B)=1,得2cos(180°-C)=1,
∴cosC=-
,
又0°<C<180°,
∴C=120°;
(2)∵a,b是方程x2-2
x+2=0的两根,
由韦达定理,得a+b=2
,ab=2,
由余弦定理,得c2=a2+b2-2abcos120°=(a+b)2-ab=12-2=10,
∴c=
;
(3)△ABC的面积S=
absinC=
×2×sin120°=
.
∴cosC=-
| 1 |
| 2 |
又0°<C<180°,
∴C=120°;
(2)∵a,b是方程x2-2
| 3 |
由韦达定理,得a+b=2
| 3 |
由余弦定理,得c2=a2+b2-2abcos120°=(a+b)2-ab=12-2=10,
∴c=
| 10 |
(3)△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查三角形面积公式、余弦定理等知识,属基础题,熟记相关公式是解题关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
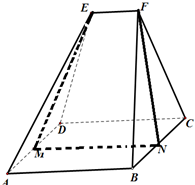 木工技艺是我国传统文化瑰宝之一,体现了劳动人民的无穷智慧.很多古代建筑和家具不用铁钉,保存到现代却依然牢固,这其中,有连接加固功能的“楔子”发挥了重要作用;如图,是一个楔子形状的直观图.其底面ABCD为一个矩形,其中AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6
木工技艺是我国传统文化瑰宝之一,体现了劳动人民的无穷智慧.很多古代建筑和家具不用铁钉,保存到现代却依然牢固,这其中,有连接加固功能的“楔子”发挥了重要作用;如图,是一个楔子形状的直观图.其底面ABCD为一个矩形,其中AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6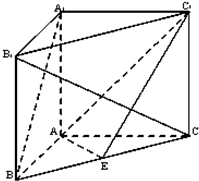 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点.