题目内容
已知数列{an}满足a1＝1，an＝a1＋
a2＋
a3＋…＋
an－1(n≥2)．
(1)求数列{an}的通项公式；
(2)若an＝2013，求n.
解析：(1)∵a1＝1，且an＝a1＋a2＋a3＋…＋an－1(n>1)．
∴a2＝a1＝1，an＋1＝a1＋a2＋a3＋…＋an－1＋
an(n≥1)．
∴an＋1－an＝an(n≥
2)．
∴an＋1＝
an，
∴
＝
(n≥2)．
∴＝
＝…＝
＝，
∴an＝
(n≥2)．
∴an＝
(2)∵an＝＝2 013，∴n＝4 026.
练习册系列答案
阅读快车系列答案
相关题目
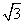)，则|u*(u＋v)|＝__
______.
{an}的前n项和为Sn，且S2＝10，S5＝55，则过点P(n，an)和Q(n＋2，an＋2)(n∈N*)的直线的斜率是( )
7 19