题目内容
当实数x,y满足
时,1≤x+ay≤5恒成立,则实数a的取值范围是 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:由约束条件作出可行域,再由1≤x+ay≤5恒成立,结合可行域内特殊点A,B,C的坐标满足不等式列不等式组,求解不等式组得实数a的取值范围.
解答:
解:由约束条件作可行域如图,
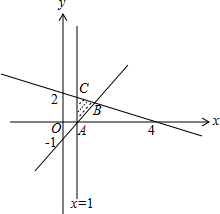 联立
联立
,解得C(1,
).
联立
,解得B(2,1).
在x-y-1=0中取y=0,得A(1,0).
要使1≤x+ay≤5恒成立,
则
,解得:1≤a≤
.
∴实数a的取值范围是[1,
].
故答案为:[1,
].
 联立
联立
|
| 3 |
| 2 |
联立
|
在x-y-1=0中取y=0,得A(1,0).
要使1≤x+ay≤5恒成立,
则
|
| 8 |
| 3 |
∴实数a的取值范围是[1,
| 8 |
| 3 |
故答案为:[1,
| 8 |
| 3 |
点评:本题考查线性规划,考查了数形结合的解题思想方法,考查了数学转化思想方法,训练了不等式组得解法,是中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
下列函数在(0,+∞)上是增函数的是( )
| A、y=9-x2 | ||
| B、y=x•log0.23+1 | ||
C、y=x
| ||
D、y=
|
设f(x)是R上的偶函数,且在[0,+∞)上是增函数,又f(1)=0,则满足f(log2x)>0的x的取值范围是( )
| A、(2,+∞) | ||
B、(0,
| ||
C、(0,
| ||
D、(
|
设
为复数z=
-i的共轭复数,(z-
)2014=( )
. |
| z |
| 1 |
| 2 |
. |
| z |
| A、22014 |
| B、-22014 |
| C、22014i |
| D、-i |
设函数f(x)=n-1,x∈[n,n+1),n∈N,函数g(x)=log2x,则方程f(x)=g(x)实数根的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
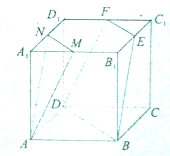 棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.
棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.