题目内容
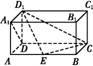
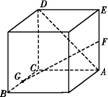
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P DEF,则四面体中异面直线PG与DH所成的角的余弦值为 .
DEF,则四面体中异面直线PG与DH所成的角的余弦值为 .
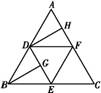
 解析:折成的正四面体,如图,连接HE,取HE的中点K,连接GK,PK.
解析:折成的正四面体,如图,连接HE,取HE的中点K,连接GK,PK.
则GK∥DH,故∠PGK(或其补角)即为所求的异面直线所成的角.
设这个正四面体的棱长为2,
在△PGK中,PG= ,GK=
,GK= ,
,
PK= =
= ,
,
故cos∠PGK=
=
= .
.
即异面直线PG与DH所成的角的余弦值是 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的最小值是( )
的最小值是( ) B.4 C.
B.4 C.  D.5
D.5 ABC的正视图、侧视图和俯视图如图所示.
ABC的正视图、侧视图和俯视图如图所示.
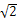 的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的表面积与体积.
的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的表面积与体积.
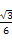
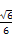
 A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.