题目内容
如图,在长方体ABCD A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
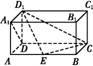
(1)求异面直线D1E与A1D所成的角;
(2)若二面角D1 EC
EC D的大小为45°,求点B到平面D1EC的距离.
D的大小为45°,求点B到平面D1EC的距离.
解:建立如图所示的空间直角坐标系.

(1)由A1(1,0,1),得
 =(1,0,1),
=(1,0,1),
设E(1,a,0),又D1(0,0,1),则 =(1,a,-1).
=(1,a,-1).
∵ ·
· =1+0-1=0,
=1+0-1=0,
∴ ⊥
⊥ ,
,
则异面直线D1E与A1D所成的角为90°.
(2)m=(0,0,1)为平面DEC的一个法向量,
设n=(x,y,z)为平面CED1的法向量,则
cos<m,n>=
=
=cos 45°
= ,
,
∴z2=x2+y2,①
由C(0,2,0),得 =(0,2,-1),
=(0,2,-1),
则n⊥ ,
,
即n· =0,
=0,
∴2y-z=0,②
由①、②,可取n=(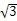 ,1,2),
,1,2),
又 =(1,0,0),
=(1,0,0),
所以点B到平面D1EC的距离
d= =
= =
= .
.

练习册系列答案
相关题目
 DEF,则四面体中异面直线PG与DH所成的角的余弦值为 .
DEF,则四面体中异面直线PG与DH所成的角的余弦值为 . 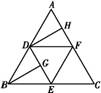
 BD
BD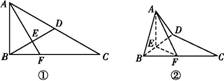
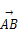 =(2,4,0),
=(2,4,0),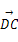 =(-1,3,0),则异面直线AB与DC所成角θ的大小为
=(-1,3,0),则异面直线AB与DC所成角θ的大小为

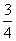 ;
;