题目内容
6.如图(1)所示,在直角梯形ABCD中,$AD∥BC,∠BAD=\frac{π}{2},AB=BC=\frac{1}{2}AD$,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.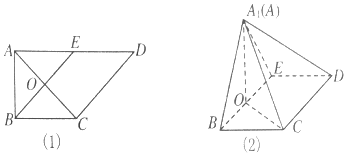
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD所成锐二面角的余弦值.
分析 (1)BE⊥平面A1OC,又BE∥CD,即可证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,以O为原点,OB,OC,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,求出平面的法向量,即可求平面A1BC与平面A1CD所成锐二面角的余弦值.
解答  (1)证明:在图(1)中,因为$AB=BC=\frac{1}{2}AD$,E是AD的中点,且$∠BAD=\frac{π}{2}$,
(1)证明:在图(1)中,因为$AB=BC=\frac{1}{2}AD$,E是AD的中点,且$∠BAD=\frac{π}{2}$,
所以BE⊥AC,BE∥CD,
即在图(2)中,BE⊥OA1,BE⊥OC,又OA1∩OC=O,OA1?平面A1OC,OC?平面A1OC,
从而BE⊥平面A1OC,又BE∥CD,所以CD⊥平面A1OC.
(2)解:由已知,平面A1BE⊥平面BCDE,且交线为BE,
又由(1)知,BE⊥OA1,所以OA1⊥平面BCDE,
如图,以O为原点,OB,OC,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
设$AB=BC=\frac{1}{2}AD=1$,所以$B(\frac{{\sqrt{2}}}{2},0,0),E(-\frac{{\sqrt{2}}}{2},0,0),{A_1}(0,0,\frac{{\sqrt{2}}}{2}),C(0,\frac{{\sqrt{2}}}{2},0)$,
得$\overrightarrow{BC}=(-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2},0),\overrightarrow{{A_1}C}=(0,\frac{{\sqrt{2}}}{2},-\frac{{\sqrt{2}}}{2}),\overrightarrow{CD}=\overrightarrow{BE}=(-\sqrt{2},0,0)$.
设平面A1BC的法向量$\overrightarrow n=({x_1},{y_1},{z_1})$,平面A1CD的法向量$\overrightarrow m=({x_2},{y_2},{z_2})$,
平面A1BC与平面A1CD的夹角为θ,
则$\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{BC}=0}\\{\overrightarrow n•\overrightarrow{{A_1}C}=0}\end{array}}\right.$得$\left\{{\begin{array}{l}{-{x_1}+{y_1}=0}\\{{y_1}-{z_1}=0}\end{array}}\right.$,取$\overrightarrow n=(1,1,1)$,同理,取$\overrightarrow m=(0,1,1)$,
从而$cosθ=|{cos<\overrightarrow n,\overrightarrow m>}|=\frac{2}{{\sqrt{2}×\sqrt{3}}}=\frac{{\sqrt{6}}}{3}$,
即平面A1BC与平面A1CD所成锐二面角的余弦值为$\frac{{\sqrt{6}}}{3}$.
点评 本题考查线面垂直的判定,考查平面A1BC与平面A1CD所成锐二面角的余弦值,考查学生向量知识的运用,属于中档题.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案| A. | 2 | B. | $\sqrt{7}$ | C. | $2\sqrt{7}$ | D. | $2\sqrt{3}$ |
| A. | -4 | B. | -3 | C. | 4 | D. | $2\sqrt{5}$ |
| A. | 40mm | B. | 40$\sqrt{10}$mm | C. | $\frac{1}{40}$mm/min | D. | $\frac{\sqrt{10}}{40}$mm/min |
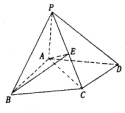 在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA⊥平面ABCD,PC与平面ABCD所成角为45°
在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA⊥平面ABCD,PC与平面ABCD所成角为45°