题目内容
2.已知函数f(x)=|x-1|+|x-a|.(1)若a≤2,解不等式f(x)≥2;
(2)若a>1,?x∈R,f(x)+|x-1|≥1,求实数a的取值范围.
分析 (1)通过讨论x的范围,求出各个区间的解集,取并集即可;(2)令F(x)=f(x)+|x-1|,求出F(x)的最小值,从而求出a的范围即可.
解答 解:(1)当f(x)=|x-1|+|x-2|=$\left\{\begin{array}{l}{-2x+3,x<1}\\{1,1≤x≤2}\\{2x-3,x>2}\end{array}\right.$,而f(x)≥2,
解得$x≤\frac{1}{2}$或$x≥\frac{5}{2}$.…(5分)
(2)令F(x)=f(x)+|x-1|,则F(x)=$\left\{\begin{array}{l}{-3x+2+a,x<1}\\{x-2+a,1≤x<a}\\{3x-2-a,x≥a}\end{array}\right.$,
所以当x=1时,F(x)有最小值F(1)=a-1,
只需a-1≥1,解得a≥2,
所以实数a的取值范围是[2,+∞).…(10分)
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
12.已知数列 {an} 的前 n 项和为Sn,S1=6,S2=4,Sn>0且S2n,S2n-1,S2n+2成等比数列,S2n-1,S2n+2,S2n+1成等差数列,则a2016等于( )
| A. | -1009 | B. | -1008 | C. | -1007 | D. | -1006 |
10.设某几何体的三视图如图所示,则该几何体的体积为( )
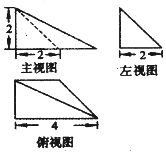

| A. | 8 | B. | 4 | C. | 2 | D. | $\frac{4}{3}$ |
17.已知平面向量$\vec a,\vec b$的夹角为$60°,\vec a=({\sqrt{3},1}),|\vec b|=1$则$|\vec a+2\vec b|$=( )
| A. | 2 | B. | $\sqrt{7}$ | C. | $2\sqrt{7}$ | D. | $2\sqrt{3}$ |
7.如果复数$\frac{2+ai}{1+2i}$的实部与虚部相等,则实数a等于( )
| A. | $\frac{2}{3}$ | B. | 6 | C. | -6 | D. | -$\frac{2}{3}$ |