题目内容
12.设函数f(x)=x+$\frac{a}{x}$+lna为定义在(-∞,0)∪(0,+∞)上的奇函数.(1)求实数a的值;
(2)判断函数f(x)在区间(1,+∞)上的单调性,并加以证明.
分析 (1)由函数f(x)=x+$\frac{a}{x}$+lna为定义在(-∞,0)∪(0,+∞)上的奇函数,可得f(-x)=-f(x),进而得到实数a的值;
(2)$f(x)=x+\frac{1}{x}$在区间(1,+∞)上是增函数,
证法一:任取1<x1<x2,作差判断出f(x1)<f(x2),根据单调性的定义,可得$f(x)=x+\frac{1}{x}$在区间(1,+∞)上是增函数,
证法二:求导,根据当x∈(1,+∞)时,f′(x)>0恒成立,得到:f(x)在区间(1,+∞)上是增函数
解答 解:(1)∵$f(x)=x+\frac{a}{x}+lna$为定义在(-∞,0)∪(0,+∞)上的奇函数,
∴f(-x)=-f(x),
∴$-x-\frac{a}{x}+lna=-(x+\frac{a}{x}+lna)$,
∴lna=0,
∴a=1.…(4分)
(2)$f(x)=x+\frac{1}{x}$在区间(1,+∞)上是增函数.…(5分)
证法一:设1<x1<x2,
则$f({x_1})-f({x_2})={x_1}-{x_2}+\frac{1}{x_1}-\frac{1}{x_2}={x_1}-{x_2}-\frac{{{x_1}-{x_2}}}{{{x_1}{x_2}}}=({x_1}-{x_2})\frac{{{x_1}{x_2}-1}}{{{x_1}{x_2}}}$.…(9分)
∵1<x1<x2,∴x1-x2<0,$\frac{{{x_1}{x_2}-1}}{{{x_1}{x_2}}}>0$.
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
∴f(x)在区间(1,+∞)上是增函数.…(12分)
证法二:∵$f(x)=x+\frac{1}{x}$,
∴$f′(x)=1-\frac{1}{{x}^{2}}$,…(9分)
当x∈(1,+∞)时,f′(x)>0恒成立,
∴f(x)在区间(1,+∞)上是增函数.…(12分)
点评 本题考查的知识点是函数的单调性,函数的奇偶性,是函数图象和性质的综合应用,难度中档.

| A. | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{10}$=1 | B. | $\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{15}$=1 | C. | $\frac{{x}^{2}}{15}$+$\frac{{y}^{2}}{10}$=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{10}$=1 |
| A. | b=-2,c=3 | B. | b=2,c=-3 | C. | b=-3,c=2 | D. | b=3,c=-2 |
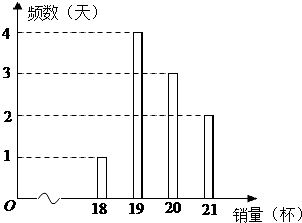 某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示:
某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示: 如图,已知AB是圆O的直径,直线CD与圆O相切于点C,弦AE的延长线交CD于点D,若∠DAC=∠CAB.
如图,已知AB是圆O的直径,直线CD与圆O相切于点C,弦AE的延长线交CD于点D,若∠DAC=∠CAB.