题目内容
已知定义域为（0，+∞）上的单调递增函数f（x），满足：?x∈（0，+∞），有f（f（x）-lnx）=1，则方程f（x）=-x2+4x-2解的个数为（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：由题意可得，存在唯一的正实数a，使f（x）-lnx=a，f（a）=1，求得a=1，可得f（x）的解析式，方程即-x2+4x-3=lnx．故方程解的个数，即函数y=-x2+4x-3的图象和函数 y=lnx 的图象的交点个数，数形结合可得结论．
解答：
解：由于定义域为（0，+∞）上的单调递增函数f（x）满足f（f（x）-lnx）=1，f（x）=-x2+4x-2，
故必存在唯一的正实数a，使f（x）-lnx=a，f（a）=1 ①，
∴f（a）-lna=a ②．
由①②求得a=1，故f（x）=1+lnx，方程f（x）=-x2+4x-2，即 1+lnx=-x2+4x-2，即-x2+4x-3=lnx．
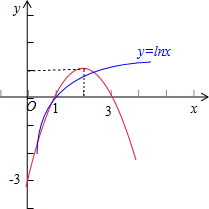
故方程解的个数即函数y=-x2+4x-3的图象和函数 y=lnx 的图象的交点个数．
数形结合可得函数y=-x2+4x-3的图象和函数 y=lnx 的图象的交点个数为3，
故选：D．
解：由于定义域为（0，+∞）上的单调递增函数f（x）满足f（f（x）-lnx）=1，f（x）=-x2+4x-2，故必存在唯一的正实数a，使f（x）-lnx=a，f（a）=1 ①，
∴f（a）-lna=a ②．
由①②求得a=1，故f（x）=1+lnx，方程f（x）=-x2+4x-2，即 1+lnx=-x2+4x-2，即-x2+4x-3=lnx．
故方程解的个数即函数y=-x2+4x-3的图象和函数 y=lnx 的图象的交点个数．
数形结合可得函数y=-x2+4x-3的图象和函数 y=lnx 的图象的交点个数为3，
故选：D．
点评：本题考查对数的运算性质的综合运用，综合性强，难度大．解题时要认真审题，注意挖掘题设中的隐含条件，合理地进行等价转化，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
设点M（m，0）在椭圆
+
=1的长轴上，点p是椭圆上任意一点． 当
的模最小时，点p恰好落在椭圆的右顶点，则实数m的取值范围（ ）
| x2 |
| 16 |
| y2 |
| 12 |
| MP |
| A、[0，4] |
| B、[1，4] |
| C、[1，5] |
| D、[3，4] |
若f（x）=x5+2x3+3x2+x+1，用秦九韶算法计算f（3）=（ ）
| A、327 | B、328 |
| C、165 | D、166 |