题目内容
5.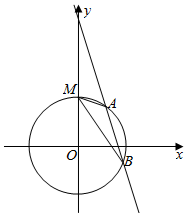 已知圆O:x2+y2=r2(r>0)与y轴的正半轴交于点M,直线l1:y=2x+1被圆O所截得的弦长为$\frac{4\sqrt{5}}{5}$,圆O上相异两动点A,B所在的直线l2的方程为y=kx+m,且满足直线MA与直线MB的斜率之积为$\frac{\sqrt{3}}{3}$.
已知圆O:x2+y2=r2(r>0)与y轴的正半轴交于点M,直线l1:y=2x+1被圆O所截得的弦长为$\frac{4\sqrt{5}}{5}$,圆O上相异两动点A,B所在的直线l2的方程为y=kx+m,且满足直线MA与直线MB的斜率之积为$\frac{\sqrt{3}}{3}$.(Ⅰ)求实数r的值;
(Ⅱ)试探究直线AB是否经过定点,若经过,请求定点的坐标;若不经过,请说明理由.
分析 (Ⅰ)由圆心O(0,0)到直线l1:y=2x+1的距离为d=$\frac{1}{\sqrt{5}}$=$\sqrt{{r}^{2}-(\frac{2\sqrt{5}}{5})^{2}}$,计算即可得到r=1;
(Ⅱ)设A(x1,y1),B(x2,y2),运用直线的斜率公式计算即可得到m的值,进而判断直线AB是否经过定点.
解答 解:(Ⅰ)∵直线l1:y=2x+1被圆O所截得的弦长为$\frac{4\sqrt{5}}{5}$,
∴圆心O(0,0)到直线l1:y=2x+1的距离为d=$\frac{1}{\sqrt{5}}$=$\sqrt{{r}^{2}-(\frac{2\sqrt{5}}{5})^{2}}$,
∴r=1;
(3)设A(x1,y1),B(x2,y2),
则x12+y12=1,x22+y22=1,
设直线AB:y=kx+m,代入x2+y2=1
∴(1+k2)x2+2kmx+m2-1=0,
∴x1+x2=-$\frac{2km}{{k}^{2}+1}$,x1x2=$\frac{{m}^{2}-1}{1+{k}^{2}}$,
则y1+y2=$\frac{2m}{{k}^{2}+1}$,y1y2=$\frac{{m}^{2}-{k}^{2}}{{k}^{2}+1}$,
∵kMA•kMB=$\frac{\sqrt{3}}{3}$
∴$\frac{{y}_{1}-1}{{x}_{1}}$•$\frac{{y}_{2}-1}{{x}_{2}}$=$\frac{\frac{{m}^{2}-{k}^{2}}{1+{k}^{2}}-\frac{2m}{1+{k}^{2}}+1}{\frac{{m}^{2}-1}{{k}^{2}+1}}$=$\frac{\sqrt{3}}{3}$
解得m=2+$\sqrt{3}$,
∴直线AB过定点(0,2+$\sqrt{3}$).
综上:直线AB过定点(0,2+$\sqrt{3}$).
点评 本题考查直线和圆的位置关系:相交,考查圆的方程的求法和直线方程联立圆的方程,运用韦达定理,以及直线的斜率公式,属于中档题.

 高中必刷题系列答案
高中必刷题系列答案| A. | [-$\frac{2}{3}$,$\frac{2}{3}$] | B. | [-$\frac{1}{3}$,$\frac{1}{3}$] | C. | [0,$\frac{2}{3}$] | D. | [0,1] |
| A. | 25 | B. | 30 | C. | 35 | D. | 40 |