题目内容
12.设函数f(x)=x2-2x-1(x≤-2).(1)求f(x)的定义域;
(2)求f(x)的值域.
分析 根据条件可求出f(x)的定义域和值域.
解答 解:(1)由已知条件可知函数的定义域为(-∞,-2];
(2)由函数f(x)=x2-2x-1的对称轴为x=1,故f(x)在(-∞,-2]单调递减,
所以f(x)max=(-2)2-2×(-2)-1=7
故函数的值域为(-∞,7].
点评 本题考查了二次函数的定义域和值域,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列函数在区间(0,+∞)上是减函数的是( )
| A. | f(x)=3x-2 | B. | f(x)=9-x2 | C. | $f(x)=\frac{1}{x-1}$ | D. | f(x)=log2x |
8.下列函数,既是奇函数又在区间(0,+∞)上单调递增的函数是( )
| A. | y=$\frac{1}{x}$ | B. | y=2|x| | C. | y=-log${\;}_{\frac{1}{2}}$x | D. | y=x|x| |
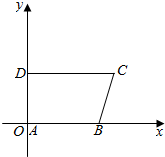 设直角梯形ABCD,DA⊥AB,在两平行边AB、DC上有两个动点P、Q,直线PQ平分梯形的面积,求证:PQ必过一个定点.
设直角梯形ABCD,DA⊥AB,在两平行边AB、DC上有两个动点P、Q,直线PQ平分梯形的面积,求证:PQ必过一个定点.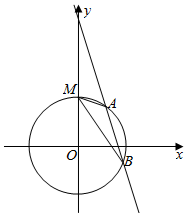 已知圆O:x2+y2=r2(r>0)与y轴的正半轴交于点M,直线l1:y=2x+1被圆O所截得的弦长为$\frac{4\sqrt{5}}{5}$,圆O上相异两动点A,B所在的直线l2的方程为y=kx+m,且满足直线MA与直线MB的斜率之积为$\frac{\sqrt{3}}{3}$.
已知圆O:x2+y2=r2(r>0)与y轴的正半轴交于点M,直线l1:y=2x+1被圆O所截得的弦长为$\frac{4\sqrt{5}}{5}$,圆O上相异两动点A,B所在的直线l2的方程为y=kx+m,且满足直线MA与直线MB的斜率之积为$\frac{\sqrt{3}}{3}$.