题目内容
17.存在实数φ,使得圆面x2+y2≤4恰好覆盖函数y=sin($\frac{π}{k}$x+φ)图象的最高点或最低点共三个,则正数k的取值范围是($\frac{\sqrt{3}}{2}$,$\sqrt{3}$].分析 由题意可得T=2k≤2$\sqrt{3}$<2T,即可解得正数k的取值范围.
解答 解:函数y=sin($\frac{π}{k}$x+φ)图象的最高点或最低点一定在直线y=±1上,
由$\left\{\begin{array}{l}{y=±1}\\{{x}^{2}+{y}^{2}≤4}\end{array}\right.$,解得:$-\sqrt{3}≤x≤\sqrt{3}$,
由题意可得:T=$\frac{2π}{\frac{π}{k}}$=2k,T≤2$\sqrt{3}$<2T,
解得正数k的取值范围是:($\frac{\sqrt{3}}{2}$,$\sqrt{3}$].
故答案为:($\frac{\sqrt{3}}{2}$,$\sqrt{3}$].
点评 本题主要考查了圆方程的综合应用,三角函数的周期性及其求法,考查了数形结合思想,属于中档题.

练习册系列答案
相关题目
8.下列函数,既是奇函数又在区间(0,+∞)上单调递增的函数是( )
| A. | y=$\frac{1}{x}$ | B. | y=2|x| | C. | y=-log${\;}_{\frac{1}{2}}$x | D. | y=x|x| |
2.下列各式的大小关系正确的是( )
| A. | sin11°>sin168° | B. | sin194°<cos160° | ||
| C. | cos(-$\frac{15π}{8}$)>cos$\frac{14π}{9}$ | D. | tan(-$\frac{π}{5}$)<tan(-$\frac{3π}{7}$) |
9.计算:lg2+lg5=( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
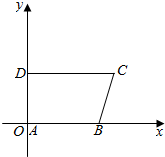 设直角梯形ABCD,DA⊥AB,在两平行边AB、DC上有两个动点P、Q,直线PQ平分梯形的面积,求证:PQ必过一个定点.
设直角梯形ABCD,DA⊥AB,在两平行边AB、DC上有两个动点P、Q,直线PQ平分梯形的面积,求证:PQ必过一个定点.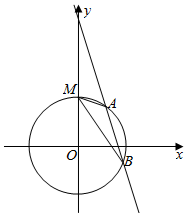 已知圆O:x2+y2=r2(r>0)与y轴的正半轴交于点M,直线l1:y=2x+1被圆O所截得的弦长为$\frac{4\sqrt{5}}{5}$,圆O上相异两动点A,B所在的直线l2的方程为y=kx+m,且满足直线MA与直线MB的斜率之积为$\frac{\sqrt{3}}{3}$.
已知圆O:x2+y2=r2(r>0)与y轴的正半轴交于点M,直线l1:y=2x+1被圆O所截得的弦长为$\frac{4\sqrt{5}}{5}$,圆O上相异两动点A,B所在的直线l2的方程为y=kx+m,且满足直线MA与直线MB的斜率之积为$\frac{\sqrt{3}}{3}$.