题目内容
13.已知O是锐角△ABC的外心,$tanA=\frac{1}{2}$.若$\frac{cosB}{sinC}•\overrightarrow{AB}+\frac{cosC}{sinB}•\overrightarrow{AC}=2m•\overrightarrow{AO}$,则实数m=$\frac{{\sqrt{5}}}{5}$.分析 设外接圆的半径为R,从而化简可得$\frac{cosB}{sinC}$($\overrightarrow{OB}$-$\overrightarrow{OA}$)•$\overrightarrow{OA}$+$\frac{cosC}{sinB}$($\overrightarrow{OC}$-$\overrightarrow{OA}$)•$\overrightarrow{OA}$=2m$\overrightarrow{AO}$•$\overrightarrow{OA}$,从而可得-2sinCcosB+(-2sinBcosC)=-2m,从而解得.
解答 解:设外接圆的半径为R,
∵$\frac{cosB}{sinC}•\overrightarrow{AB}+\frac{cosC}{sinB}•\overrightarrow{AC}=2m•\overrightarrow{AO}$,
∴$\frac{cosB}{sinC}$($\overrightarrow{OB}$-$\overrightarrow{OA}$)+$\frac{cosC}{sinB}$($\overrightarrow{OC}$-$\overrightarrow{OA}$)=2m$\overrightarrow{AO}$,
∵∠AOB=2∠C,∠AOC=2∠B,
∴$\frac{cosB}{sinC}$($\overrightarrow{OB}$-$\overrightarrow{OA}$)•$\overrightarrow{OA}$+$\frac{cosC}{sinB}$($\overrightarrow{OC}$-$\overrightarrow{OA}$)•$\overrightarrow{OA}$=2m$\overrightarrow{AO}$•$\overrightarrow{OA}$,
即$\frac{cosB}{sinC}$•R2•(cos2C-1)+$\frac{cosC}{sinB}$•R2•(cos2B-1)=-2mR2,
即-2sinCcosB+(-2sinBcosC)=-2m,
故sinCcosB+sinBcosC=m,
故sin(B+C)=m,
故m=sinA=$\frac{{\sqrt{5}}}{5}$,
故答案为:$\frac{{\sqrt{5}}}{5}$.
点评 本题考查了正弦定理的应用,同时考查了平面向量数量积的应用及三角恒等变换的应用,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | f(x)=3x-2 | B. | f(x)=9-x2 | C. | $f(x)=\frac{1}{x-1}$ | D. | f(x)=log2x |
| A. | y=$\frac{1}{x}$ | B. | y=2|x| | C. | y=-log${\;}_{\frac{1}{2}}$x | D. | y=x|x| |
| A. | sin11°>sin168° | B. | sin194°<cos160° | ||
| C. | cos(-$\frac{15π}{8}$)>cos$\frac{14π}{9}$ | D. | tan(-$\frac{π}{5}$)<tan(-$\frac{3π}{7}$) |
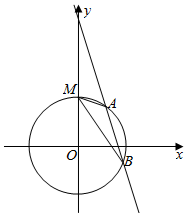 已知圆O:x2+y2=r2(r>0)与y轴的正半轴交于点M,直线l1:y=2x+1被圆O所截得的弦长为$\frac{4\sqrt{5}}{5}$,圆O上相异两动点A,B所在的直线l2的方程为y=kx+m,且满足直线MA与直线MB的斜率之积为$\frac{\sqrt{3}}{3}$.
已知圆O:x2+y2=r2(r>0)与y轴的正半轴交于点M,直线l1:y=2x+1被圆O所截得的弦长为$\frac{4\sqrt{5}}{5}$,圆O上相异两动点A,B所在的直线l2的方程为y=kx+m,且满足直线MA与直线MB的斜率之积为$\frac{\sqrt{3}}{3}$.