题目内容
函数f(x)=x2+ax+3,x∈[-2,2].
(1)若a=2,求f(x)的最值,并说明当f(x)取最值时的x的值;
(2)若f(x)≥a恒成立,求a的取值范围.
(1)若a=2,求f(x)的最值,并说明当f(x)取最值时的x的值;
(2)若f(x)≥a恒成立,求a的取值范围.
考点:二次函数在闭区间上的最值
专题:综合题,函数的性质及应用
分析:(1)利用配方法,结合函数的单调性,即可求f(x)的最值;
(2)对于[-2,2]区间内的任意x恒成立,按区间与对称轴的关系分三种情况讨,最后结合图象即可解决问题.
(2)对于[-2,2]区间内的任意x恒成立,按区间与对称轴的关系分三种情况讨,最后结合图象即可解决问题.
解答:
解:(1)f(x)=x2+2x+3=(x+1)2+2,
∵x∈[-2,2],
∴x=-1时,函数取得最小值2;x=2时,函数取得最大值11;
(2)当x∈[-2,2]时,设g(x)=x2+ax+3-a≥0,
分如下三种情况讨论(如图所示):
①如图(1),当g(x)的图象恒在x轴上方时,满足条件时,有△=a2-4(3-a)≤0,即-6≤a≤2.
②如图(2),g(x)的图象与x轴有交点,
当-
≤-2时,g(x)≥0,即
解之得a∈Φ.
③如图(3),g(x)的图象与x轴有交点,
-
≥-2时,g(x)≥0,即
,解之得-7≤a≤-6
综合①②③得a∈[-7,2].
∵x∈[-2,2],
∴x=-1时,函数取得最小值2;x=2时,函数取得最大值11;
(2)当x∈[-2,2]时,设g(x)=x2+ax+3-a≥0,
分如下三种情况讨论(如图所示):
①如图(1),当g(x)的图象恒在x轴上方时,满足条件时,有△=a2-4(3-a)≤0,即-6≤a≤2.
②如图(2),g(x)的图象与x轴有交点,

当-
| a |
| 2 |
|
解之得a∈Φ.
③如图(3),g(x)的图象与x轴有交点,
-
| a |
| 2 |
|
综合①②③得a∈[-7,2].
点评:本题主要了一元二次不等式恒成立的问题,注考查利用了二次函数图象的特点数形结合解决问题,属于中档题.

练习册系列答案
相关题目
在△ABC中,“△ABC是锐角三角形”是“sinA>cosB”的( )
| A、充分必要条件 |
| B、充分而不必要条件 |
| C、必要而不充分条件 |
| D、既不充分又不必要条件 |
已知复数z满足z•i=3+4i,则z=( )
| A、-4-3i | B、-4+3i |
| C、4+3i | D、4-3i |
下列函数在区间(0,+∞)上为增函数的是( )
| A、y=1-2x | ||
| B、y=x2+2x | ||
| C、y=-x2 | ||
D、y=
|
 阅读如图的程序框图,运行相应的程序,则输出S的值为
阅读如图的程序框图,运行相应的程序,则输出S的值为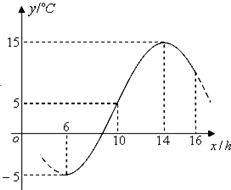 如图,某地一天6-16时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,其中A>0,ω>0,0<φ<π.
如图,某地一天6-16时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,其中A>0,ω>0,0<φ<π.