题目内容
已知不等式x2-2x+1-a2<0(a>0)成立的一个充分条件是0<x<4,则实数a的取值范围是 .
考点:充分条件
专题:简易逻辑
分析:求出不等式的等价条件,根据充分条件和必要条件的定义即可得到结论.
解答:
解:∵x2-2x+1-a2<0(a>0),
∴[x-(1-a)][x-(1+a)]<0,
则1-a<x<1+a,
∵不等式x2-2x+1-a2<0(a>0)成立的一个充分条件是0<x<4,
∴
,即
,
解得a≥3;
故答案为:a≥3
∴[x-(1-a)][x-(1+a)]<0,
则1-a<x<1+a,
∵不等式x2-2x+1-a2<0(a>0)成立的一个充分条件是0<x<4,
∴
|
|
解得a≥3;
故答案为:a≥3
点评:本题主要考查充分条件和必要条件的应用,根据不等式的性质求解不等式的等价条件是解决本题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
当m<0时,复数2+m•i在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
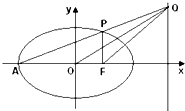 如图,在平面直角坐标系xOy中,已知A,F分别为椭圆C:
如图,在平面直角坐标系xOy中,已知A,F分别为椭圆C: