题目内容
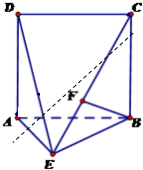 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.(Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求点D到平面ACE的距离;
(Ⅲ)求二面角E-AC-B的余弦值.
考点:二面角的平面角及求法,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知得BF⊥AE,CB⊥AE,由此能证明AE⊥平面BCE.
(Ⅱ)设D到平面ACE的距离为h,由VD-ACE=VE-ACD,能求出点D到平面ACE的距离.
(Ⅲ)作BO⊥AC于O,连接OF,则∠BOF=θ为所求二面角的平面角,由此能求出二面角E-AC-B的余弦值.
(Ⅱ)设D到平面ACE的距离为h,由VD-ACE=VE-ACD,能求出点D到平面ACE的距离.
(Ⅲ)作BO⊥AC于O,连接OF,则∠BOF=θ为所求二面角的平面角,由此能求出二面角E-AC-B的余弦值.
解答:
(Ⅰ)证明:∵BF⊥平面ACE,∴BF⊥AE,(1分)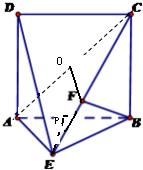
∵二面角D-AB-E为直二面角,且CB⊥AB,∴CB⊥平面ABE.(3分)
∴CB⊥AE,又CB∩BF=B,
∴AE⊥平面BCE.(4分)
(Ⅱ)解:过点E作EP⊥AB,交AB于点P,PE=1.(5分)
∵二面角D-AB-E为直二面角,∴EP⊥平面ABCD.(6分)
设D到平面ACE的距离为h,
∵VD-ACE=VE-ACD,
∴
S△ACE•h=
S△ACD•EP,(7分)
∵AE⊥平面BCE,∴AE⊥EC,
∴h=
=
,(8分)
∴点D到平面ACE的距离为
.(9分)
(Ⅲ)解:作BO⊥AC于O,连接OF,则∠BOF=θ为所求二面角的平面角.(10分)
且BF⊥OF,COSθ=
,(11分)
在等腰直角三角形ABC中,O为AC中点,
OB=0.5AC=
,OC=
,CE=
.(12分)
由△COF∽△CEA,知
=
,OF=
•AE=
,(13分)
故COSθ=
=
.(14分)

∵二面角D-AB-E为直二面角,且CB⊥AB,∴CB⊥平面ABE.(3分)
∴CB⊥AE,又CB∩BF=B,
∴AE⊥平面BCE.(4分)
(Ⅱ)解:过点E作EP⊥AB,交AB于点P,PE=1.(5分)
∵二面角D-AB-E为直二面角,∴EP⊥平面ABCD.(6分)
设D到平面ACE的距离为h,
∵VD-ACE=VE-ACD,
∴
| 1 |
| 3 |
| 1 |
| 3 |
∵AE⊥平面BCE,∴AE⊥EC,
∴h=
| ||||||
|
2
| ||
| 3 |
∴点D到平面ACE的距离为
2
| ||
| 3 |
(Ⅲ)解:作BO⊥AC于O,连接OF,则∠BOF=θ为所求二面角的平面角.(10分)
且BF⊥OF,COSθ=
| OF |
| OB |
在等腰直角三角形ABC中,O为AC中点,
OB=0.5AC=
| 2 |
| 2 |
| 6 |
由△COF∽△CEA,知
| OF |
| AE |
| OC |
| CE |
| OC |
| CE |
| ||
| 3 |
故COSθ=
| OF |
| OB |
| ||
| 3 |
点评:本题考查AE⊥平面BCE的证明,考查点D到平面ACE的距离的求法,考查二面角E-AC-B的余弦值的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程|log2x-2|+1=|log2x|的解集是( )
| A、{2,8} | |||||
B、{2
| |||||
C、{
| |||||
D、{2,
|
若函数f(x)=
是R上的减函数,则a的取值范围( )
|
A、a<
| ||||
B、a≤
| ||||
C、
| ||||
D、0<a<
|
自二面角α-l-β的棱l上任选一点O,若∠AOB是二面角α-l-β的平面角,必须具备条件( )
| A、AO⊥OB,AO?α,BO?β |
| B、AO⊥l,BO⊥l |
| C、AB⊥l,AO?α,BO?β |
| D、AO⊥l,OB⊥l,AO?α,BO?β |
