题目内容
已知函数f(x)=
+a(a∈R)为奇函数,函数g(x)=m•2x-m.
(1)求函数f(x)的解析式;
(2)判断函数f(x)在x∈(0,+∞)的单调性并用定义证明;
(3)若在区间(-∞,0)上,y=f(x)的图象恒在y=g(x)的图象的下方,试确定实数m的范围.
| 1 |
| 2x-1 |
(1)求函数f(x)的解析式;
(2)判断函数f(x)在x∈(0,+∞)的单调性并用定义证明;
(3)若在区间(-∞,0)上,y=f(x)的图象恒在y=g(x)的图象的下方,试确定实数m的范围.
考点:函数的最值及其几何意义,函数解析式的求解及常用方法,函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:(1)由题意,f(-x)=
+a=-(
+a);从而解a;从而得到函数f(x)的解析式;
(2)先判断,后用复合函数的单调性证明;
(3)在区间(-∞,0)上,y=f(x)的图象恒在y=g(x)的图象的下方可化为
<0在区间(-∞,0)上恒成立;从而化为最值问题.
| 1 |
| 2-x-1 |
| 1 |
| 2x-1 |
(2)先判断,后用复合函数的单调性证明;
(3)在区间(-∞,0)上,y=f(x)的图象恒在y=g(x)的图象的下方可化为
| 2x-2m(2x-1)2 |
| 2(2x-1) |
解答:
解:(1)∵f(x)=
+a为奇函数,
∴f(-x)=
+a=-(
+a);
则2a=-
-
=1;
故a=
;
则f(x)=
+
;
(2)f(x)在x∈(0,+∞)上是减函数,证明如下,
∵y=2x-1在(0,+∞)上是增函数,且y>0;
又∵y=
在(0,+∞)上是减函数,
故f(x)=
+
在(0,+∞)上是减函数.
(3)f(x)-g(x)=
+
-m(2x-1)
=
,
∵在区间(-∞,0)上,y=f(x)的图象恒在y=g(x)的图象的下方,
∴
<0在区间(-∞,0)上恒成立;
∵2x-1<0,
故2x-2m(2x-1)2>0;
故m<
;
令F(x)=
=
,
∵x∈(-∞,0),
∴2x∈(0,1);
∴
>0;
故m≤0.
| 1 |
| 2x-1 |
∴f(-x)=
| 1 |
| 2-x-1 |
| 1 |
| 2x-1 |
则2a=-
| 1 |
| 2x-1 |
| 1 |
| 2-x-1 |
=1;
故a=
| 1 |
| 2 |
则f(x)=
| 1 |
| 2x-1 |
| 1 |
| 2 |
(2)f(x)在x∈(0,+∞)上是减函数,证明如下,
∵y=2x-1在(0,+∞)上是增函数,且y>0;
又∵y=
| 1 |
| x |
故f(x)=
| 1 |
| 2x-1 |
| 1 |
| 2 |
(3)f(x)-g(x)=
| 1 |
| 2x-1 |
| 1 |
| 2 |
=
| 2x-2m(2x-1)2 |
| 2(2x-1) |
∵在区间(-∞,0)上,y=f(x)的图象恒在y=g(x)的图象的下方,
∴
| 2x-2m(2x-1)2 |
| 2(2x-1) |
∵2x-1<0,
故2x-2m(2x-1)2>0;
故m<
| 2x |
| 2(2x-1)2 |
令F(x)=
| 2x |
| 2(2x-1)2 |
| 1 | ||
2(2x+
|
∵x∈(-∞,0),
∴2x∈(0,1);
∴
| 1 | ||
2(2x+
|
故m≤0.
点评:本题考查了函数的性质的应用及恒成立问题,属于中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
直线ax-2y-1=0和直线2y-3x+b=0平行,则直线y=ax+b和直线y=3x+1的位置关系是( )
| A、平行 | B、重合 |
| C、平行或重合 | D、相交 |
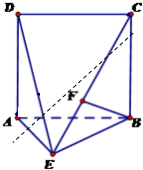 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.