题目内容

若函数f（x）=
(3a-1)x+4a(x＜1)
logax(x≥1)
是R上的减函数，则a的取值范围（　　）
A、a＜
1
3
B、a≤
1
3
C、
1
7
≤a＜
1
3
D、0＜a＜
1
3
考点：函数单调性的性质
专题：函数的性质及应用
分析：根据单调性利用最值大小，转化为
0＜a＜1
3a-1＜0
7a-1≥0
即得出；
1
7
≤a＜
1
3
，即可得出答案．
解答： 解：∵函数f（x）=
(3a-1)x+4a(x＜1)
logax(x≥1)
是R上的减函数，
∴
0＜a＜1
3a-1＜0
7a-1≥0
即得出；
1
7
≤a＜
1
3
，
故选：C
点评：本题综合考查了函数的单调性，转化为不等式组求解即可，属于中档题．
练习册系列答案
相关题目
等式1+2+3+…+n=
n(n+1)
2
证明过程如下：
①当n=1时，左边=1，右边=1等式成立；
②假设当n=k时等式成立，即1+2+3+…+k=
k(k+1)
2
，那么当n=k+1时，1+2+3+…+k+（k+1）=
k(k+1)
2
+(k+1)=
(k+1)[(k+1)+1]
2
等式也成立，故原等式成立，以上证明方法是（　　）
A、分析法B、综合法
C、反证法D、数学归纳法
已知矩形ABCD，|AB|=4，|AD|=1，点O为线段AB的中点．动点P沿矩形ABCD的边从B逆时针运动到A．当点P运动过的路程为x时，记点P的运动轨迹与线段OP、OB围成的图形面积为f（x）．
（1）求f（x）表达式；
（2）若f（x）=2，求x的值．
如图，正方体的棱长为2，试建立适当的空间直角坐标系，写出正方体各顶点的坐标及各边中点的坐标．
如果-
1
4
a＞-
1
3
b，则
1
4
a＜
1
3
b．
 
（判断对错）．
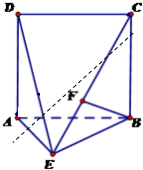如图，直二面角D-AB-E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE．
（Ⅰ）求证：AE⊥平面BCE；
（Ⅱ）求点D到平面ACE的距离；
（Ⅲ）求二面角E-AC-B的余弦值．
棱长为1的正方体ABCD-A′B′C′D′，P为棱CC′上一点，Q为AD中点．
（1）当PC为何值时，AP⊥A′Q；
（2）在（1）的情况下，求异面直线A′B与AP所成的角．
求值：[（-3）2] 
3
2
-（
1
2
）-1+log0.57+log212-
1
2
log242+log2
7
48
．
已知函数
f(x)=
3x(x＞0)
2(x=0)
x+5(x≤0)
，则f{f[f（-5）]}=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网