题目内容
已知定义域为R的函数f(x)=
是奇函数.
(Ⅰ)求a,b的取值.
(Ⅱ)若对任意实数t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求实数k的取值范围.
| -2x+b |
| 2x+1+a |
(Ⅰ)求a,b的取值.
(Ⅱ)若对任意实数t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求实数k的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用
分析:(Ⅰ)由已知得f(0)=
=0,f(1)=-f(-1),由此能求出a,b.
(Ⅱ)f(x)=
=-
+
,从而f(t2-2t)+f(2t2-k)<0等价于f(t2-2t)<-f(2t2-k)=f(-2t2+k),由此能求出k<-
.
| -1+b |
| 2+a |
(Ⅱ)f(x)=
| -2x+1 |
| 2x+1+2 |
| 1 |
| 2 |
| 1 |
| 2x+1 |
| 1 |
| 3 |
解答:
解:(Ⅰ)∵f(x)=
是奇函数,
∴f(0)=
=0,解得b=1.
从而有f(x)=
,
又由f(1)=-f(-1)知
=-
,解得a=2.
(Ⅱ)由(Ⅰ)知f(x)=
=-
+
,
由上式易知f(x)在(-∞,+∞)上为减函数,
又因f(x)是奇函数,
从而不等式f(t2-2t)+f(2t2-k)<0等价于f(t2-2t)<-f(2t2-k)=f(-2t2+k),
因f(x)是减函数,由上式推得t2-2t>-2t2+k,
即对一切t∈R有3t2-2t-k>0,
从而判别式△=4+12k<0,解得k<-
.
| -2x+b |
| 2x+1+a |
∴f(0)=
| -1+b |
| 2+a |
从而有f(x)=
| -2x+1 |
| 2x+1+a |
又由f(1)=-f(-1)知
| -2+1 |
| 4+a |
-
| ||
| 1+a |
(Ⅱ)由(Ⅰ)知f(x)=
| -2x+1 |
| 2x+1+2 |
| 1 |
| 2 |
| 1 |
| 2x+1 |
由上式易知f(x)在(-∞,+∞)上为减函数,
又因f(x)是奇函数,
从而不等式f(t2-2t)+f(2t2-k)<0等价于f(t2-2t)<-f(2t2-k)=f(-2t2+k),
因f(x)是减函数,由上式推得t2-2t>-2t2+k,
即对一切t∈R有3t2-2t-k>0,
从而判别式△=4+12k<0,解得k<-
| 1 |
| 3 |
点评:本题考查实数值的求法,考查实数的取值范围的求法,解题时要认真审题,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
为得到函数y=sin2x的图象,只需将函数y=cos(x+
)的图象( )
| π |
| 3 |
A、横坐标变为原来2倍,再向右平移
| ||||
B、横坐标变为原来2倍,再向右平移
| ||||
C、横坐标变为原来
| ||||
D、横坐标变为原来
|
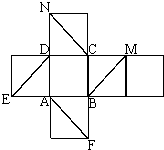 如图是正方体的平面展开图,在这个正方体中,①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是
如图是正方体的平面展开图,在这个正方体中,①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是