题目内容
10.已知△ABC的内角A,B,C的对边分别为a,b,c,若b2=a2+c2-ac,ac=4,则△ABC的面积为( )| A. | 1 | B. | 2$\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$ |
分析 由已知及余弦定理可得cosB的值,结合范围B∈(0,π),可求B,利用三角形面积公式即可计算得解.
解答 解:∵b2=a2+c2-ac,
∴由余弦定理可得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{ac}{2ac}$=$\frac{1}{2}$,
∵B∈(0,π),
∴B=$\frac{π}{3}$,
∵ac=4,
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}×4×\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
故选:D.
点评 本题主要考查了余弦定理,三角形面积公式在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
2.2017×2016×2015×2014×…×1978×1977等于( )
| A. | C${\;}_{2017}^{40}$ | B. | C${\;}_{2017}^{41}$ | C. | A${\;}_{2017}^{40}$ | D. | A${\;}_{2017}^{41}$ |
 的图象过点
的图象过点 ,则
,则 的值为( )
的值为( )
 D.
D.
 ,则
,则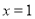 ”的逆否命题为“若
”的逆否命题为“若 ,则
,则 ”;
”; ”是“
”是“ ”的充分不必要条件;
”的充分不必要条件; 是假命题,则
是假命题,则 均为假命题;
均为假命题; ,使得
,使得 ,则
,则 为:
为: ,均有
,均有