题目内容
5.已知函数f(x)=$\frac{1}{3}$x3-2x2+3x+b(b∈R).(Ⅰ)当b=0时,求f(x)在[1,4]上的值域;
(Ⅱ)若函数f(x)有三个不同的零点,求b的取值范围.
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,求出函数的值域即可;
(Ⅱ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,求出函数的极大值和极小值,根据函数的零点的个数,得到b的范围即可.
解答 解:(Ⅰ)当b=0时,f(x)=$\frac{1}{3}$x3-2x2+3x,
f′(x)=x2-4x+3=(x-1)(x-3),
x∈[1,3)时,f′(x)<0,函数f(x)在[1,3)递减,
x∈(3,4]时,f′(x)>0,函数f(x)在(3,4]递增,
由f(3)=0,f(1)=f(4)=$\frac{4}{3}$,
∴f(x)在[1,4]的值域是[0,$\frac{4}{3}$];
(Ⅱ)由(Ⅰ)可知,f′(x)=(x-1)(x-3),
由f′(x)<0,解得:1<x<3,
由f′(x)>0,解得:x>3或x<1,
故f(x)在(1,3)递减,在(-∞,1),(3,+∞)递增,
故f(x)极大值=f(1)=b+$\frac{4}{3}$,f(x)极小值=f(3)=b,
故b+$\frac{4}{3}$>0且b<0即-$\frac{4}{3}$<b<0时,函数f(x)有三个不同的零点.
点评 本题考查了函数的单调性、极值,最值问题,考查导数的应用以及转化思想,是一道中档题.

练习册系列答案
相关题目
17.函数f(x)=cos(2x+φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{6}$个单位后得到的函数是奇函数,则函数f(x)的图象( )
| A. | 关于点(-$\frac{π}{3}$,0)对称 | B. | 关于直线x=-$\frac{π}{6}$对称 | ||
| C. | 关于点($\frac{π}{12}$,0)对称 | D. | 关于直线x=$\frac{π}{12}$对称 |
1.用数学归纳法证明“1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{n}-1}$<n(n≥2)”时,由n=k的假设证明n=k+1时,不等式左边需增加的项数为( )
| A. | 2k-1 | B. | 2k-1 | C. | 2k | D. | 2k+1 |
10.已知△ABC的内角A,B,C的对边分别为a,b,c,若b2=a2+c2-ac,ac=4,则△ABC的面积为( )
| A. | 1 | B. | 2$\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$ |
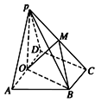 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PDA⊥底面ABCD,O是AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PDA⊥底面ABCD,O是AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$. ,
, 满足条件
满足条件 则
则 的最大值是( )
的最大值是( ) 的方程
的方程 ,有两个不同的实根,则实数
,有两个不同的实根,则实数 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.