题目内容
3.已知函数f(x)是周期为2的函数,当-1≤x≤1时,f(x)=|x|,则当函数y=f(x)-kx(k>0)有四个零点时.实数k的取值范围是($\frac{1}{5}$,$\frac{1}{3}$).分析 由条件作出f(x)的图象,考虑直线y=kx经过点A(3,1),B(5,1),求得k,结合图象和条件,即可得到所求k的范围.
解答  解:函数f(x)是周期为2的函数,
解:函数f(x)是周期为2的函数,
当-1≤x≤1时,f(x)=|x|,
作出f(x)的图象如右:
当直线y=kx经过点A(3,1),可得k=$\frac{1}{3}$;
当直线y=kx经过点B(5,1),可得k=$\frac{1}{5}$.
由题意当函数y=f(x)-kx(k>0)有四个零点时,
即y=f(x)的图象与直线y=kx有4个交点,
则$\frac{1}{5}$<k<$\frac{1}{3}$.
故答案为:($\frac{1}{5}$,$\frac{1}{3}$).
点评 本题考查函数的零点问题解法,注意运用转化思想和方程思想,以及数形结合思想方法,考查运算能力,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
8.若复数z=$\frac{i}{-1+i}$,则复数z的模为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 2 |
10.已知△ABC的内角A,B,C的对边分别为a,b,c,若b2=a2+c2-ac,ac=4,则△ABC的面积为( )
| A. | 1 | B. | 2$\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$ |
 中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美,给出定义:能够将圆B的周长和面积同时平分的函数称为这个圆的“优美函数”,给出下列命题:
中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美,给出定义:能够将圆B的周长和面积同时平分的函数称为这个圆的“优美函数”,给出下列命题: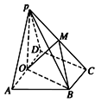 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PDA⊥底面ABCD,O是AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PDA⊥底面ABCD,O是AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$. 的展开式中
的展开式中 的系数是 .(用数字作答)
的系数是 .(用数字作答)