题目内容
函数f(x)=sinx+cosx的最小正周期为 ,单调增区间为 ,f(-
)= .
| π |
| 12 |
考点:正弦函数的图象,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:利用辅助角公式将三角函数进行化简即可得到结论.
解答:
解:f(x)=sinx+cosx=
sin(x+
),
则函数的周期T=
=2π,
由2kπ-
≤x+
≤2kπ+
,k∈Z,
解得2kπ-
≤x≤2kπ+
,k∈Z,
故函数的递增区间为[2kπ-
,2kπ+
],
f(-
)=
sin(-
+
)=
sin
=
×
=
,
故答案为:2π,[2kπ-
,2kπ+
],
.
| 2 |
| π |
| 4 |
则函数的周期T=
| 2π |
| 1 |
由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
解得2kπ-
| 3π |
| 4 |
| π |
| 4 |
故函数的递增区间为[2kπ-
| 3π |
| 4 |
| π |
| 4 |
f(-
| π |
| 12 |
| 2 |
| π |
| 12 |
| π |
| 4 |
| 2 |
| π |
| 6 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
故答案为:2π,[2kπ-
| 3π |
| 4 |
| π |
| 4 |
| ||
| 2 |
点评:本题主要考查三角函数的图象和性质,利用辅助角公式进行化简是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
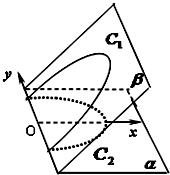 如右图二面角α-y-β的大小为60°,平面β上的曲线C1在平面α上的正射影为曲线C2,C2在直角坐标系xOy下的方程x2+y2=1(0≤x≤1),则曲线C1的离心率( )
如右图二面角α-y-β的大小为60°,平面β上的曲线C1在平面α上的正射影为曲线C2,C2在直角坐标系xOy下的方程x2+y2=1(0≤x≤1),则曲线C1的离心率( )| A、e=1 | ||||
| B、e>1 | ||||
C、e=
| ||||
D、e=
|
若全集U=R,集合A={x|x2+x-2≤0},B={y|y=log2(x+3),x∈A},则集合A∩(∁UB)=( )
| A、{x|-2≤x<0} |
| B、{x|0≤x≤1} |
| C、{x|-3<x≤-2} |
| D、{x|x≤-3} |
在半径为R球面上有A,B,C三点,且AB=8
,∠ACB=60°,球心O到平面ABC的距离为6,则半径R=( )
| 3 |
| A、8 | B、10 | C、12 | D、14 |