题目内容
2.下列有关命题的说法正确的是( )| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | 线性回归直线方程y=bx+a恒过样本中心$(\overline x,\overline y)$,且至少经过一个样本点 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 |
分析 A.根据否命题的定义进行判断.
B.根据线性回归方程的性质进行判断.
C.根据含有量词的命题的否定进行判断.
D.根据逆否命题的等价性进行判断.
解答 解:A.命题“若x2=1,则x=1”的否命题为:“若x2≠1,则x≠1”故A错误,
B.线性回归直线方程y=bx+a恒过样本中心$(\overline x,\overline y)$,但不一定过样本点,故B错误,
C.命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1≥0”,故C错误,
D.若x=y,则sinx=siny成立,即原命题成立,则命题的逆否命题为真命题,故D正确,
故选:D
点评 本题主要考查命题的真假判断,涉及四种命题的关系,含有量词的命题的否定,以及线性回归直线方程的性质,比较基础.

练习册系列答案
相关题目
14.已知函数y=sin(ωx+$\frac{π}{3}$)向右平移$\frac{π}{3}$个单位后,所得的图象与原函数图象关于x轴对称,则ω的最小正值为( )
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
11.如图所示,正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,以下四个结论中正确的是( )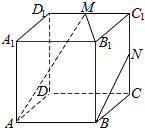

| A. | 直线MN与DC1互相垂直 | B. | 直线AM与BN互相平行 | ||
| C. | 直线MN与BC1所成角为90° | D. | 直线MN垂直于平面A1BCD1 |
12.若函数f(x)=x2+ax+$\frac{1}{x}$在[$\frac{1}{3}$,+∞)上是增函数,则实数a的取值范围是( )
| A. | [-1,0] | B. | [0,$\frac{25}{3}$] | C. | [$\frac{25}{3}$,+∞) | D. | [9,+∞) |
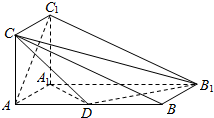 如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.