题目内容
9.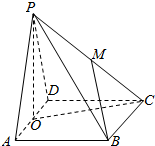 已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是边长为2的正三角形,平面ABCD⊥平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值是( )
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAD是边长为2的正三角形,平面ABCD⊥平面PAD,M是PC的中点,O是AD的中点,则直线BM与平面PCO所成角的正弦值是( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{\sqrt{2}}{3}$ |
分析 以O为原点,OA为x轴,过O作AB平行线为y轴,OP为z轴,建立空间直角坐标系,利用向量法能求出直线BM与平面PCO所成角的正弦值.
解答 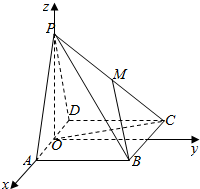 解:以O为原点,OA为x轴,过O作AB平行线为y轴,OP为z轴,建立空间直角坐标系,
解:以O为原点,OA为x轴,过O作AB平行线为y轴,OP为z轴,建立空间直角坐标系,
B(1,2,0),P(0,0,$\sqrt{3}$),C(-1,2,0),M(-$\frac{1}{2}$,1,$\frac{\sqrt{3}}{2}$),O(0,0,0),
$\overrightarrow{OP}$=(0,0,$\sqrt{3}$),$\overrightarrow{OC}$=(-1,2,0),$\overrightarrow{BM}$=(-$\frac{3}{2}$,-1,$\frac{\sqrt{3}}{2}$),
设平面PCO的法向量$\overrightarrow{n}$=(x,y,z),
$\left\{\begin{array}{l}{\overrightarrow{OP}•\overrightarrow{n}=\sqrt{3}z=0}\\{\overrightarrow{OC}•\overrightarrow{n}=-x+2y=0}\end{array}\right.$,取x=2,得$\overrightarrow{n}$=(2,1,0),
设直线BM与平面PCO所成角为θ,
则sinθ=$\frac{|\overrightarrow{BM}•\overrightarrow{n}|}{|\overrightarrow{BM}|•|\overrightarrow{n}|}$=$\frac{4}{\sqrt{4}•\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$.
∴直线BM与平面PCO所成角的正弦值是$\frac{2\sqrt{5}}{5}$.
故选:B.
点评 本题考查线面角的正弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
| A. | $\widehat{y}$=0.4x+0.9 | B. | $\widehat{y}$=2x-5.5 | C. | $\widehat{y}$=-2x+10.5 | D. | $\widehat{y}$=-0.3x+4.7 |
| A. | 充分不必要条件 | B. | 必要且不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |