题目内容
19.已知$\overrightarrow a,\overrightarrow b$满足:$\left|{\overrightarrow a}\right|=2,\left|{\overrightarrow b}\right|=1,\left|{\overrightarrow a-\overrightarrow b}\right|=\sqrt{6}$,则$\left|{\overrightarrow a+\overrightarrow b}\right|$( )| A. | $\sqrt{3}$ | B. | $\sqrt{10}$ | C. | 3 | D. | 2 |
分析 利用(a+b)2=2(a2+b2)-(a-b)2,从而代入化简即可.
解答 解:∵$\left|{\overrightarrow a}\right|=2,\left|{\overrightarrow b}\right|=1,\left|{\overrightarrow a-\overrightarrow b}\right|=\sqrt{6}$,
∴$\left|{\overrightarrow a+\overrightarrow b}\right|$2=2($|\overrightarrow{a}|$2+$|\overrightarrow{b}|$2)-$|\overrightarrow{a}-\overrightarrow{b}|$2
=2(4+1)-6=4,
∴$\left|{\overrightarrow a+\overrightarrow b}\right|$=2,
故选:D.
点评 本题考查了完全平方公式的应用及平面向量数量积的应用.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
18.-90°+k•360°(k∈z)表示的是( )
| A. | 第一象限角 | B. | 第三象限角 | C. | 界限角 | D. | 第四象限角 |
14.已知函数y=sin(ωx+$\frac{π}{3}$)向右平移$\frac{π}{3}$个单位后,所得的图象与原函数图象关于x轴对称,则ω的最小正值为( )
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
11.如图所示,正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,以下四个结论中正确的是( )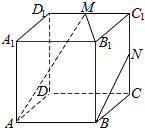

| A. | 直线MN与DC1互相垂直 | B. | 直线AM与BN互相平行 | ||
| C. | 直线MN与BC1所成角为90° | D. | 直线MN垂直于平面A1BCD1 |
8.已知α∈(-$\frac{π}{2}$,0),且cosα=$\frac{\sqrt{5}}{5}$,则sin(π+2α)等于( )
| A. | $\frac{1}{5}$ | B. | -$\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
9.已知抛物线x2=2py(p>0),斜率为1的直线交抛物线于A,B两点,若线段AB中点的横坐标为2,则该抛物线的准线方程为( )
| A. | y=-1 | B. | y=1 | C. | y=-2 | D. | y=2 |
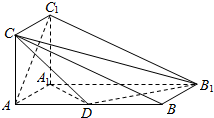 如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.