题目内容
16.求1356和2400的最小公倍数271200.分析 本题考查的知识点是辗转相除法,根据辗转相除法的步骤,将1356和2400代入求出两个数的最大公约数,进而可得最小公倍数.
解答 解:∵2400=1356×1+1044,
1356=1044×1+312,
1044=312×3+108,
312=108×2=96,
108=96×1+12,
96=12×6,
故1356和2400的最大公约数为12,
故1356和2400的最小公倍数为1356×2400÷12=271200,
故答案为:271200.
点评 本题考查的知识点是最大公约数和最小公倍数,正确理解最大公约数和最小公倍数的积,等于两个数据的积,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知a<b<0,则下列不等式成立的是( )
| A. | a2<b2 | B. | $\frac{a}{b}<1$ | C. | a<1-b | D. | $\frac{1}{a}<\frac{1}{b}$ |
5.已知f(x)=ax+btanx+3,且f(-3)=7,则f(3)=( )
| A. | 4 | B. | -1 | C. | -7 | D. | 9 |
6.如果α是第二象限的角,下列各式中成立的是( )
| A. | tanα=-$\frac{sinα}{cosα}$ | B. | cosα=-$\sqrt{1-si{n}^{2}α}$ | C. | sinα=-$\sqrt{1-co{s}^{2}α}$ | D. | tanα=$\frac{cosα}{sinα}$ |
 在某批次的某种灯泡中,随机地抽取500个样品,并对其寿命进行追踪调查,将结果列成频率分布直方图如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.
在某批次的某种灯泡中,随机地抽取500个样品,并对其寿命进行追踪调查,将结果列成频率分布直方图如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.
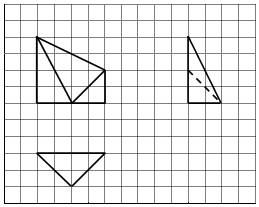 如图,网格纸上每个正方形小格的边长为1,图中粗线画出的是某多面体的三视图,则该几何体的表面中互相垂直的平面有( )
如图,网格纸上每个正方形小格的边长为1,图中粗线画出的是某多面体的三视图,则该几何体的表面中互相垂直的平面有( )