题目内容
8.已知sinα=2cosα,求sin2α+2sinαcosα的值.分析 化简所求的表达式为正切函数的形式,代入求解即可.
解答 解:∵sinα=2cosα,可得:tanα=2,
∴sin2α+2sinαcosα=$\frac{si{n}^{2}α+2sinαcosα}{si{n}^{2}α+co{s}^{2}α}$=$\frac{ta{n}^{2}α+2tanα}{ta{n}^{2}α+1}$=$\frac{4+2×2}{4+1}$=$\frac{8}{5}$.
点评 本题考查三角函数化简求值,同角三角函数的基本关系式的应用,是基础题.

练习册系列答案
相关题目
18.某几何体的三视图如图所示,则该几何体的体积是( )


| A. | $\frac{4π}{3}$ | B. | $\frac{5π}{3}$ | C. | $2+\frac{2π}{3}$ | D. | $4+\frac{2π}{3}$ |
3.方程-x3+x2+x-2=0的根的分布情况是( )
| A. | 一个根,在(-∞,-$\frac{1}{3}$)内 | B. | 两个根,分别在(-∞,-$\frac{1}{3}$)、(0,+∞)内 | ||
| C. | 三个根,分别在(-∞,-$\frac{1}{3}$)、(-$\frac{1}{3}$,0),(1,+∞) | D. | 三个根,分别在(-∞,-$\frac{1}{3}$),(0,1),(1,+∞)内 |
13.生于瑞士的数学巨星欧拉在1765年发表的《三角形的几何学》一书中有这样一个定理:“三角形的外心、垂心和重心都在同一直线上,而且外心和重心的距离是垂心和重心距离之半.”这就是著名的欧拉线定理.设△ABC中,设O、H、G分别是外心、垂心和重心,下列四个选项锥误的是( )
| A. | HG=2OG | B. | $\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$ | ||
| C. | 设BC边中点为D,则有AH=3OD | D. | S△ABG=S△BCG=S△ACG |
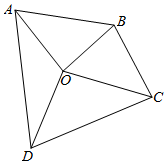 如图,为了测量学校操场四边形ABCD的周长和面积,在操场中间取一点O.测得OA=40m,OB=37m,OC=42m,OD=44m,且∠DOA=120°,∠AOB=80°,∠BOC=60°,∠COD=100°.
如图,为了测量学校操场四边形ABCD的周长和面积,在操场中间取一点O.测得OA=40m,OB=37m,OC=42m,OD=44m,且∠DOA=120°,∠AOB=80°,∠BOC=60°,∠COD=100°.