题目内容
曲线f(x)=ex-2x+1在点(0,f(0))处的切线方程为x+ay-b=0,则a+b等于( )
| A、-l | B、1 | C、-3 | D、3 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:欲求曲线f(x)=ex-2x+1在点(0,f(0))处的切线方程,只须求出其斜率即可,故先利用导数求出在x=0处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
解答:
解:∵f(x)=ex-2x+1,
∴f′(x)=ex,-2,
∴曲线f(x)=ex-2x+1在点(0,f(0))处的切线的斜率为:k=e0-2=-1,
∵f(0)=2
∴曲线f(x)=ex-2x+1在点(0,f(0))处的切线方程为:y-2=-x,即x+y-2=0,
∵曲线f(x)=ex-2x+1在点(0,f(0))处的切线方程为x+ay-b=0,
∴a=1,b=2,
∴a+b=3.
故选:D.
∴f′(x)=ex,-2,
∴曲线f(x)=ex-2x+1在点(0,f(0))处的切线的斜率为:k=e0-2=-1,
∵f(0)=2
∴曲线f(x)=ex-2x+1在点(0,f(0))处的切线方程为:y-2=-x,即x+y-2=0,
∵曲线f(x)=ex-2x+1在点(0,f(0))处的切线方程为x+ay-b=0,
∴a=1,b=2,
∴a+b=3.
故选:D.
点评:本题主要考查利用导数研究曲线上某点切线方程、直线方程的应用等基础知识,考查运算求解能力.属于基础题.

练习册系列答案
相关题目
已知角θ为第四象限角,且tanθ=-
,则sinθ+cosθ=( )
| 3 |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
如图程序,输出的结果A是( )


| A、5 | B、6 | C、15 | D、120 |
在△ABC中,边a,b,c的对角分别为A,B,C,若a2=b2+c2+
bc,则A的大小为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
已知向量
=(1,2),
=(x,-6),若
∥
,则x的值为( )
| a |
| b |
| a |
| b |
| A、-3 | B、3 | C、12 | D、-12 |
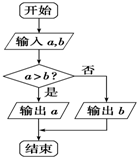 如图所示的程序框图,其功能是( )
如图所示的程序框图,其功能是( )| A、输入a,b的值,按从小到大的顺序输出它们的值 |
| B、输入a,b的值,按从大到小的顺序输出它们的值 |
| C、求a,b的最大值 |
| D、求a,b的最小值 |
数列0.9,0.99,0.999,0.9999,…的一个通项公式是( )
A、an=1-
| ||
B、an=1-
| ||
C、an=1-
| ||
D、an=1-
|
 如图,ABCD为正四面体,AD⊥面α于点A,点B、C、D均在平面α外,且在平面α的同一侧,线段BC的中点为E,则直线AE与平面α所成角的正弦值为( )
如图,ABCD为正四面体,AD⊥面α于点A,点B、C、D均在平面α外,且在平面α的同一侧,线段BC的中点为E,则直线AE与平面α所成角的正弦值为( )